已知: 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 =(1,2)
=(1,2)
⑴若| |
|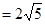 ,且
,且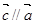 ,求
,求 的坐标;
的坐标;
⑵若| |=
|=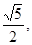 且
且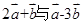 垂直,求
垂直,求 与
与 的夹角θ。
的夹角θ。
设函数
(1)当 时,求函数
时,求函数 的最大值;
的最大值;
(2)令 (
( )其图象上任意一点
)其图象上任意一点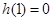 处切线的斜率
处切线的斜率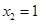 ≤
≤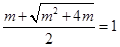 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当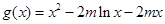 ,
, ,方程
,方程 有唯一实数解,求正数
有唯一实数解,求正数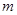 的值.
的值.
如图,某市准备在一个湖泊的一侧修建一条直路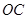 ,另一侧修建一条观光大道,它的前一段
,另一侧修建一条观光大道,它的前一段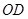 是以
是以 为顶点,
为顶点, 轴为对称轴,开口向右的抛物线的一部分,后一段
轴为对称轴,开口向右的抛物线的一部分,后一段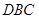 是函数
是函数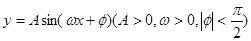 ,
,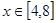 时的图象,图象的最高点为
时的图象,图象的最高点为 ,
, ,垂足为
,垂足为 .
.
(1)求函数 的解析式;
的解析式;
(2)若在湖泊内修建如图所示的矩形水上乐园 ,问:点
,问:点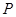 落在曲线
落在曲线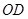 上何处时,水上乐园的面积最大?
上何处时,水上乐园的面积最大?
设函数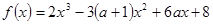 ,其中
,其中 .
.
(1)若 在
在 处取得极值,求常数
处取得极值,求常数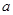 的值;
的值;
(2)设集合 ,
,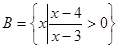 ,若
,若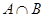 元素中有唯一的整数,求
元素中有唯一的整数,求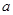 的取值范围.
的取值范围.
已知函数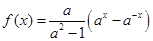 ,其中
,其中
(1)写出 的奇偶性与单调性(不要求证明);
的奇偶性与单调性(不要求证明);
(2)若函数 的定义域为
的定义域为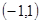 ,求满足不等式
,求满足不等式 的实数
的实数 的取值集合;
的取值集合;
(3)当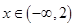 时,
时,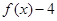 的值恒为负,求
的值恒为负,求 的取值范围.
的取值范围.