如图1，两个不全等的等腰直角三角形
和
叠放在一起，并且有公共的直角顶点
．
（1）在图1中，你发现线段
，
的数量关系是 ，直线，相交成 度角．
（2）将图1中的
绕点顺时针旋转
角，这时（1）中的两个结论是否成立？请做出判断并说明理由．
（3）将图1中的绕点顺时针旋转一个锐角，得到图3，这时（1）中的两个结论是否成立？请作出判断并说明理由．
如图（1）是某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，桥洞与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m的景观灯．现把拱桥的截面图放在平面直角坐标系中，如图（2）．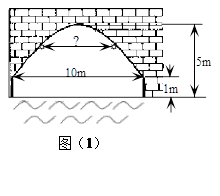
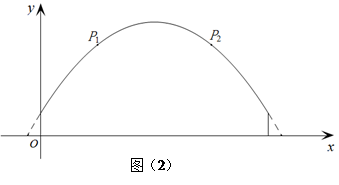
求（1）抛物线的解析式；
（2）两盏景观灯P1、P2之间的水平距离.
如图，一艘海轮位于灯塔P的南偏东60º方向，距离灯塔100海里的A处，它计划沿正北方向航行，去往位于灯塔P的北偏东45º方向上的B处.（参考数据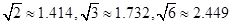
）
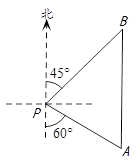
（1）问B处距离灯塔P有多远？（结果精确到0.1海里）
（2）假设有一圆形暗礁区域，它的圆心位于射线PB上，距离灯塔190海里的点O处.圆形暗礁区域的半径为50海里，进入这个区域，就有触礁的危险.请判断海轮到达B处是否有触礁的危险，并说明理由.
如图，△ABC是⊙O的内接三角形，⊙O的直径BD交AC于点E，AF⊥BD与点F，延长AF交BC于点G.求证：AB2=BG·BC
如图，一次函数y1=x+1的图象与反比例函数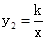
（k为常数，且
）的图象都经过点A(m,2).
（1）求点A的坐标及反比例函数的解析式；
（2）观察图象，当x>0时，直接写出y1与y2的大小关系.
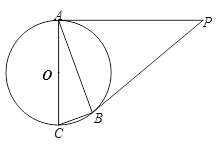
如图，PA﹑PB是⊙O的切线，A﹑B 是切点，AC是⊙O的直径，∠ACB=70º.求∠P的度数.