(本小题14分)某人有楼房一幢,室内面积共计180m2,拟分割成两类房间作为旅游客房,大房间每间面积为18m2,可住游客5名,每名游客每天住宿费40元;小房间每间面积为15m2,可以住游客3名,每名游客每天住宿费50元;装修大房间每间需要1000元,装修小房间每间需要600元.如果他只能筹款8000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,每天能获得最大的房租收益?(注:设分割大房间为x间,小房间为y间,每天的房租收益为z元)
(1)写出x,y所满足的线性约束条件;
(2)写出目标函数的表达式;
(3)求x,y各为多少时,每天能获得最大的房租收益?每天能获得最大的房租收益是多少?
已知椭圆
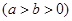 上的动点到焦点距离的最小值为
上的动点到焦点距离的最小值为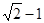 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线 相切.
相切.
(Ⅰ)求椭圆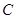 的方程;
的方程;
(Ⅱ)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆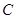 相交于
相交于 两点,
两点, 为椭圆上一点, 且满足
为椭圆上一点, 且满足 (
(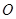 为坐标原点),当
为坐标原点),当 时,求实数
时,求实数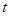 的值.
的值.
某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金 (单位:万元)随销售利润
(单位:万元)随销售利润 (单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的
(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的 %.现有三个奖励模型:
%.现有三个奖励模型: ,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注:
,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注: )
)
设函数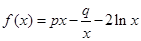 ,且
,且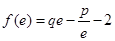 ,其中
,其中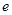 是自然对数的底数.
是自然对数的底数.
(1)求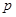 与
与 的关系;
的关系;
(2)若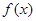 在其定义域内为单调函数,求
在其定义域内为单调函数,求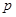 的取值范围.
的取值范围.
设 ,
,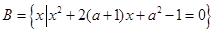 ,且B
,且B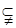 A,求实数
A,求实数 的取值范围.
的取值范围.
设函数 ,(
,( )
)
(I)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)当 时,求
时,求 的最大值.
的最大值.