设计求解一元二次方程 的一个算法,并用流程图表示。
的一个算法,并用流程图表示。
(本小题12分)如图,已知 平面
平面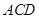 ,
,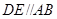 ,
,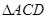 为等边三角形,
为等边三角形,
 ,
, 为
为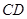 的中点.
的中点.
(1)求证: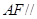 平面
平面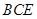 ;
;
(2)求证:平面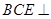 平面
平面 ;
;
(3)求直线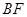 和平面
和平面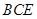 所成角的正弦值.
所成角的正弦值.
(本小题12分)为丰富高三学生的课余生活,提升班级的凝聚力,某校高三年级6个班(含甲、乙)举行唱歌比赛.比赛通过随机抽签方式决定出场顺序.
求:(1)甲、乙两班恰好在前两位出场的概率;
(2)比赛中甲、乙两班之间的班级数记为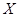 ,求
,求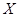 的分布列和数学期望.
的分布列和数学期望.
(本小题12分)已知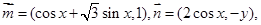 满足
满足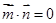 .
.
(1)将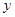 表示为
表示为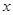 的函数
的函数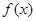 ,并求
,并求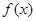 的单调递增区间;
的单调递增区间;
(2)已知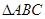 三个内角
三个内角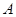 、
、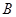 、
、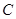 的对边分别为
的对边分别为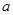 、
、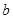 、
、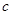 ,若
,若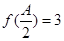 ,且
,且 ,求
,求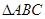 面积的最大值.
面积的最大值.
如图,在正方体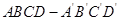 中,点
中,点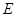 是
是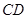 的中点.
的中点.
(1) 求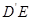 与
与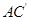 所成的角的余弦值;
所成的角的余弦值;
(2) 求直线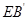 与平面
与平面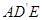 所成的角的余弦值.
所成的角的余弦值.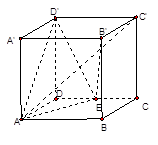
某小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(I)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(II)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,该小组没有参加过数学研究性学习活动的同学个数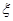 是一个随机变量,求随机变量
是一个随机变量,求随机变量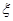 的分布列及数学期望
的分布列及数学期望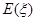 .
.