(本小题满分14分)已知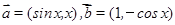 ,
,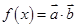 且
且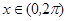 ,记
,记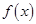 在
在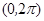 内零点为
内零点为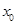 .
.
(1)求当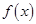 取得极大值时,
取得极大值时,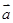 与
与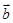 的夹角θ.
的夹角θ.
(2)求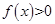 的解集.
的解集.
(3)求当函数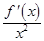 取得最小值时
取得最小值时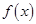 的值,并指出向量
的值,并指出向量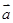 与
与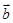 的位置关系.
的位置关系.
四棱锥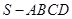 中,底面
中,底面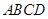 为平行四边形,侧面
为平行四边形,侧面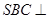 面
面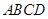 ,已知
,已知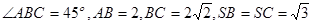
(Ⅰ)求证: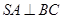 ;
;
(Ⅱ)在SB上选取点P,使SD//平面PAC ,并证明;
(Ⅲ)求直线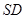 与面
与面 所成角的正弦值。
所成角的正弦值。
(本小题满分12分)
一个不透明的袋子中装有4个形状相同的小球,分别标有不同的数字2,3,4,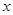 ,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
| 摸球总次数 |
10 |
20 |
30 |
60 |
90 |
120 |
180 |
240 |
330 |
450 |
| “和为7”出现的频数 |
1 |
9 |
14 |
24 |
26 |
37 |
58 |
82 |
109 |
150 |
| “和为7”出现的频率 |
0.10 |
0.45 |
0.47 |
0.40 |
0.29 |
0.31 |
0.32 |
0.34 |
0.33 |
0.33 |
(参考数据: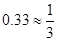 )
)
(Ⅰ)如果试验继续下去,根据上表数据,出现“数字之和为7”的频率将稳定在它的概率附近。试估计“出现数字之和为7”的概率,并求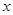 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,设定一种游戏规则:每次摸2球,若数字和为7,则可获得奖金7元,否则需交5元。某人摸球3次,设其获利金额为随机变量 元,求
元,求 的数学期望和方差。
的数学期望和方差。
已知向量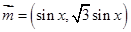 ,
,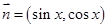 ,设函数
,设函数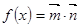 .
.
(Ⅰ)求函数 的解析式,并求
的解析式,并求 在区间
在区间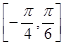 上的最小值;
上的最小值;
(Ⅱ)在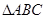 中,
中,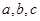 分别是角
分别是角 的对边,
的对边,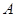 为锐角,若
为锐角,若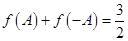 ,
,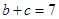 ,
,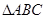 的面积为
的面积为 ,求
,求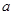 .
.
已知函数
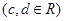 ,其图象为曲线
,其图象为曲线 ,点
,点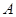 为曲线
为曲线 上的动点,在点
上的动点,在点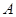 处作曲线
处作曲线 的切线
的切线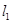 与曲线
与曲线 交于另一点
交于另一点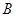 ,在点
,在点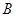 处作曲线
处作曲线 的切线
的切线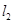 .
.
(Ⅰ)当 时,求函数
时,求函数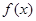 的单调区间;
的单调区间;
(Ⅱ)当点 时,
时,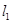 的方程为
的方程为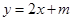 ,求实数
,求实数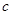 和
和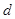 的值;
的值;
(Ⅲ)设切线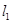 、
、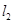 的斜率分别为
的斜率分别为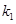 、
、 ,试问:是否存在常数
,试问:是否存在常数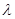 ,使得
,使得 ?若存在,求出
?若存在,求出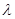 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在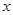 轴上,离心率
轴上,离心率 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线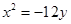 的焦点.
的焦点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 与曲线
与曲线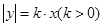 的交点为
的交点为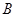 、
、 ,求
,求 面积的最大值.
面积的最大值.