(本小题满分12分)在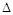 ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=
ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=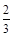 ,sinB=
,sinB=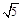 cosC.
cosC.
(Ⅰ)求tanC的值;
(Ⅱ)若a=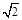 ,求
,求 ABC的面积
ABC的面积
已知函数f(x)=(x-a)2(x-b)(a,b∈R,a<b).
(1)当a=1,b=2时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2.证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后构成等差数列,并求x4.
如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.
(1)证明:B,D,H,E四点共圆;
(2)证明:CE平分∠DEF.
如图,两条相交线段 、
、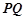 的四个端点都在抛物线
的四个端点都在抛物线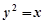 上,其中,直线
上,其中,直线 的方程为
的方程为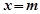 ,直线
,直线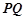 的方程为
的方程为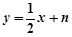 .
.
(1)若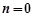 ,
,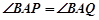 ,求
,求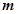 的值;
的值;
(2)探究:是否存在常数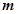 ,当
,当 变化时,恒有
变化时,恒有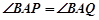 ?
?
设函数 ,
,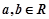 ,
,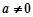 .
.
(1)若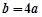 ,求
,求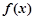 的单调递增区间;
的单调递增区间;
(2)若曲线 与
与 轴相切于异于原点的一点,且
轴相切于异于原点的一点,且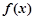 的极小值为
的极小值为 ,求
,求 的值.
的值.
已知四棱锥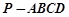 的底面是平行四边形,
的底面是平行四边形,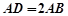 ,
,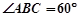 ,
,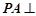 面
面 ,且
,且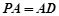 .若
.若 为
为 中点,
中点, 为线段
为线段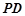 上的点,且
上的点,且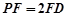 .
.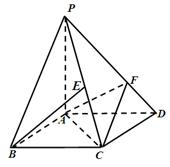
(1)求证: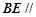 平面
平面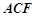 ;
;
(2)求PC与平面PAD所成角的正弦值.