如图,一架云梯长25米,斜靠在一面墙上,梯子底端离墙7米。
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑4米,那么梯子的底部在水平方向也滑动了4米吗?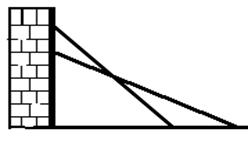
(8分)某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成统计图(如图). 
(1)在A出口的被调查游客中,购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的___,
(2)试问A出口的被调查游客在园区内人均购买了多少瓶饮料?
(3)已知B、C两个出口的被调查游客在园区内人均购买饮料的数量如下表所示
| 出口 |
B |
C |
| 人均购买饮料数量(瓶) |
3 |
2 |
若C出口的被调查人数比B出口的被调查人数多2万,且B、C两个出口的被调查游客在园区内共购买了49万瓶饮料,试问B出口的被调查游客有多少万人?
(8分)解方程:
(1)3x+(-2x+1)-(4x-2)=6(2)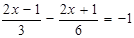
某校组织七年级学生参加社会实践活动,如果单独租用45座客车若干辆,则刚好坐满;如果单独租用60座客车,则可少租1辆,并且剩余15个座位.
(1)该校参加社会实践活动有多少人?
(2)已知45座客车的日租金为每辆1000元,60座客车的日租金为每辆1200元,该校租用哪种车更合算?
如图,已知平面上有四个点A 、B、C、D.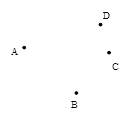
(1)连结AB,并画出AB的中点E;
(2)作射线AD;
(3)作直线BC与射线AD交于点F.
先化简,再求值:(本题8分)
2(x2y+xy2)-2(x2y-x)-2xy2-2y的值,其中x=-2,y=1