杭州湾跨海大桥于2008年5月1日通车,从此宁波到上海有了更便捷的通道,而无需再绕道杭州,实现了节时、节能.下表是宁波到上海两条线路的有关数据:
| 线路 |
弯路(宁波—杭州—上海) |
直路(宁波—跨海大桥—上海) |
| 路程 |
316千米 |
196千米 |
| 过路费 |
140元 |
180元 |
⑴若小车的平均速度为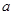 千米/小时,则小车走直路比走弯路节省多少时间?
千米/小时,则小车走直路比走弯路节省多少时间?
⑵当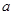 为80千米/小时,则小车走直路比走弯路节省多少时间?
为80千米/小时,则小车走直路比走弯路节省多少时间?
⑶若小车每千米的油耗为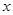 升,汽油价格为5.00元/升,小车走直路和走弯路的总费用分别为
升,汽油价格为5.00元/升,小车走直路和走弯路的总费用分别为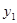 元、
元、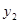 元,试用
元,试用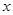 的代数式表示
的代数式表示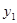 、
、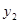 (总费用=过路费+油耗费).
(总费用=过路费+油耗费).
(1)计算: ;
;
(2)化简: .
.
如图,半径为2的⊙C与x轴的正半轴交于点A,与y轴的正半轴交于点B,点C的坐标为(1,0)若抛物线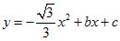 过A.B两点.
过A.B两点.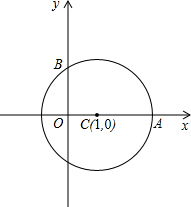
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠PBO=∠POB? 若存在求出P的坐标,不存在说明理由;
(3)若点M是抛物线(在第一象限内的部分)上一点,△MAB面积为S,求S的最大(小)值.
如图,已知直线PA交⊙O于A.B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CDPA⊥,垂足为D. 
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
如图,平行四边形ABCD中, ,点
,点 的坐标是
的坐标是 ,以点
,以点 为顶点的抛物线
为顶点的抛物线 经过
经过 轴上的点
轴上的点 .
.
(1)求点 的坐标;
的坐标;
(2)若抛物线向上平移后恰好经过点 ,求平移后抛物线的解析式.
,求平移后抛物线的解析式.
已知:如图,AB是⊙O的直径,点C.D为圆上两点,且弧CB=弧CD,CF⊥AB于点F,CE⊥AD的延长线于点E.
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求△ACD的面积.