(本小题满分14分)
已知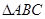 ,内角
,内角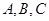 所对的边分别为
所对的边分别为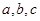 ,且满足下列三个条件:①
,且满足下列三个条件:①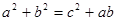 ②
② ③
③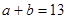
求: (1) 内角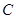 和边长
和边长 的大小; (2)
的大小; (2) 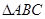 的面积.
的面积.
设f(x)=x3+ax2+bx+1的导数f′(x)满足f′(1)=2a,f′(2)=﹣b,其中常数a,b∈R.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程.
(2)设g(x)=f′(x)e﹣x.求函数g(x)的极值.
某市公租房的房源位于A、B、C三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任4位申请人中:
(1)恰有2人申请A片区房源的概率;
(2)申请的房源所在片区的个数的ξ分布列与期望.
设α∈R,f(x)=cosx(asinx﹣cosx)+cos2( ﹣x)满足
﹣x)满足 ,求函数f(x)在
,求函数f(x)在 上的最大值和最小值.
上的最大值和最小值.
设实数数列{an}的前n项和Sn满足Sn+1=an+1Sn(n∈N*).
(1)若a1,S2,﹣2a2成等比数列,求S2和a3.
(2)求证:对k≥3有0≤ak≤ .
.
设函数
(1)若
为
的极值点,求实数
;
(2)求实数
的取值范围,使得对任意的
,恒有
成立.注:e为自然对数的底数.