如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动.
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且BE=3cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?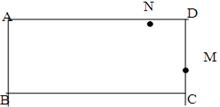
如图,在一滑梯侧面示意图中,BD∥AF,BC⊥AF于点C,DE⊥AF于
点E.BC=1.8m,BD=0.5m,∠A=45º,∠F=29º.
(1)求滑道DF的长(精确到0.1m);
(2)求踏梯AB底端A与滑道DF底端F的距离AF(精确到0.1m).
(参考数据:sin29º≈0.48,cos29º≈0.87,tan29º≈0.55)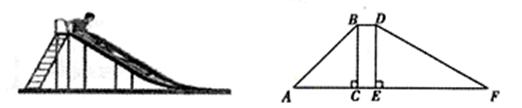
(6分 )某市为了提高学生的安全防范意识和能力,每年在全市中小学学生中举
)某市为了提高学生的安全防范意识和能力,每年在全市中小学学生中举
行安全知识竞赛,为了了解今年全市七年级同学的竞赛成绩情况,小强随机调查了一些七年
级同学的竞赛成绩,根据收集到的数据绘制了参与调查学生成绩的频数分布直方图和其中合
格学生成绩的扇形统计图如下: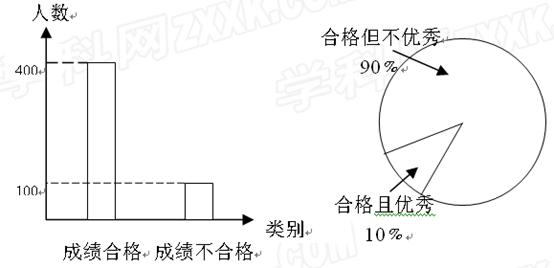
根据统计图提供的信息,解答以下问题:
(1)小强本次共调查了多少名七年级同学的成绩?被调查的学生中成绩合格的频率是多少?
(2)该市若有10000名七年级学生,请你根据小强的调查统计结果估计全市七年级学生中有多少名学生竞赛成绩合格?对此你有何看法?
(3)填写下表:
| 成绩 |
不合格 |
合格但不优秀 |
合格且优秀 |
| 频率 |
0.2 |
▲ |
▲ |
先化简,再求值: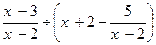 ,其中
,其中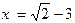 .
.
如图,已知直角梯形ABCD中,AD//BC, DC⊥BC,AB=5,BC=6, ∠B=53°.点O为BC边上的一个点,连结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,连结MN.
∠B=53°.点O为BC边上的一个点,连结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,连结MN.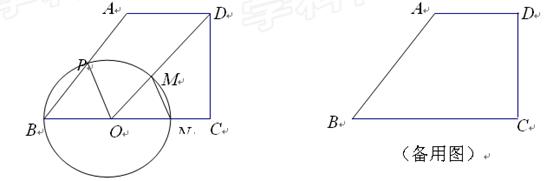
(1)当BO=AD时,求BP的长;
(2)在点O运动的 过程中,线段 BP与MN能否相等?若能,请求出当BO为多长时BP=MN;若不能,请说明理由;
过程中,线段 BP与MN能否相等?若能,请求出当BO为多长时BP=MN;若不能,请说明理由;
(3)在点O运动的过程中,以点C为圆心,CN为半径作⊙C,请直接写出当⊙C存在时,⊙O与⊙C的位置关系,以及相应的⊙C半径CN的取值范围.
(参考数据:cos5 3°≈0.6;sin53°≈0.8;t
3°≈0.6;sin53°≈0.8;t an74°
an74°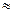 3.5)
3.5)
(10分)某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共l00个,设做竖式纸盒x个.
①根据题意,完成以下表格:
 纸盒 纸盒纸板 |
竖式纸盒(个) |
横式纸盒(个) |
 x x |
100-x |
|
| 正方形纸板(张) |
▲ |
2(100-x) |
| 长方形纸板(张) |
4x |
▲ |
②按两种纸盒的生产个数来分,有哪几种生产方案?
(2)若有正方形纸162张,长方形纸板a张,做成上述 两种纸盒,纸板恰好用完.已知290<a<306.求 a的值.
两种纸盒,纸板恰好用完.已知290<a<306.求 a的值.