如图，在方格纸上建立平面直角坐标系，线段AB的两个端点都在格点上，直线MN经过坐标原点，且点M的坐标是(1，2)｡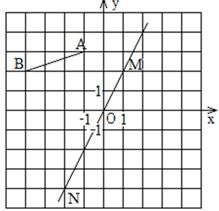
(1)写出点A、B的坐标；
(2)求直线MN所对应的函数关系式；
(3)利用尺规作出线段AB关于直线MN的对称图形(保留作图痕迹，不写作法)｡
小明在初三上学期的数学成绩如下表所示:
| 测验类别 |
平时 |
期中 考试 |
期末 考试 |
|||
| 测验1 |
测验2 |
测验3 |
测验4 |
|||
| 成绩 |
88 |
72 |
98 |
86 |
90 |
85 |
(1)计算小明上学期平时的平均成绩；
(2)如果学期的总评成绩按右图所示的比例计算；请计算出小明该学期的总评成绩.
小林在初三第一学期的数学书面测验成绩如下:平时考试第一单元得84分,第二单位得76分,第三单元得92分;期中考试得82分,期末考试得90分,如果按照平时、期中、期末的权重分别为10%,30%,60%计算,那么小林该学期数学书面测验的总评成绩应为多少分?
在“心系灾区”自愿捐款活动中,某班30名同学的捐款情况如下表:
| 捐款(元) |
5 |
10 |
15 |
20 |
25 |
30 |
| 人数 |
11 |
9 |
6 |
2 |
1 |
1 |
⑴问这个班级捐款总数是多少元?
⑵求这30名同学捐款的平均数｡
一辆经营长途运输的货车在高速公路的
处加满油后匀速行驶,下表记录的是货车一次加满油后油箱内余油量
(升)与行驶时间
(时)之间的关系:
| 行驶时间(时) |
0 |
1 |
2 |
2.5 |
| 余油量(升) |
100 |
80 |
60 |
50 |
(1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示与之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
(2)按照(1)中的变化规律,货车从处出发行驶4.2小时到达B处,求此时油箱内余油多少升?
某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售｡按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题
| 土特产种类 |
甲 |
乙 |
丙 |
| 每辆汽车运载量(吨) |
8 |
6 |
5 |
| 每吨土特产获利(百元) |
12 |
16 |
10 |
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式；
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案；
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值｡