已知函数f(x)=(x2+ax+2)ex,(x,a∈R).
(1)当a=0时,求函数f(x)的图象在点A(1,f(1))处的切线方程;
(2)若函数y=f(x)为单调函数,求实数a的取值范围;
(3)当 时,求函数f(x)的极小值.
时,求函数f(x)的极小值.
如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=

(1)求证:AO 平面BCD,(2)求异面直线AB与CD所成角的大小,(3)求两面角O—AC—D的大小。
平面BCD,(2)求异面直线AB与CD所成角的大小,(3)求两面角O—AC—D的大小。
已知数列 。
。
(I)证明:数列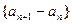 是等比数列,并求出数列
是等比数列,并求出数列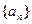 的通项公式;
的通项公式;
(II)记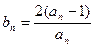 ,数列
,数列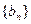 的前n项和为
的前n项和为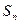 ,求使
,求使 的n的最小值。
的n的最小值。
某公司是否对某一项目投资,由甲、乙、丙三位决策人投票决定,他们三人都有“同意”、“中立”、“反对”三类票各一张,投票时,每人必须且只能投一张票,每人投三类票中的任何一类的概率都是 ,他们的投票相互没有影响。规定:若投票结果中至少有2张“同意”票,则决定对该项目投资,否则放弃投资。(Ⅰ)求此公司决定对该项目投资的概率;(Ⅱ)求此公司放弃对该项目投资且投票结果中最多有一张“中立”票的概率.
,他们的投票相互没有影响。规定:若投票结果中至少有2张“同意”票,则决定对该项目投资,否则放弃投资。(Ⅰ)求此公司决定对该项目投资的概率;(Ⅱ)求此公司放弃对该项目投资且投票结果中最多有一张“中立”票的概率.
已知向量 ,函数
,函数 。
。
(I)求函数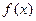 的最小正周期和值域.(II)在
的最小正周期和值域.(II)在 中.a,b,c分别是角A,B,C的对边,且
中.a,b,c分别是角A,B,C的对边,且 且
且 ,求a,b的值.
,求a,b的值.
在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为A(-1,0),B(1,0),平面
内两点G,M同时满足下列条件① +
+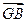 +
+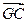 =0;②|
=0;②| |=|
|=| |=|
|=|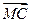 |;③
|;③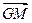 ∥
∥ .(Ⅰ)求△ABC的顶点C的轨迹方程;(Ⅱ)是否存在过点P(3,0)的直线l与(Ⅰ)中轨迹交于E、F两点,且OE⊥OF?若存在,求出直线l斜率k的值;若不存在,说明理由.
.(Ⅰ)求△ABC的顶点C的轨迹方程;(Ⅱ)是否存在过点P(3,0)的直线l与(Ⅰ)中轨迹交于E、F两点,且OE⊥OF?若存在,求出直线l斜率k的值;若不存在,说明理由.