本题12分)
已知函数 .
.
(1)求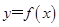 的定义域;
的定义域;
(2)在函数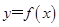 的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
的图象上是否存在不同的两点,使得过这两点的直线平行于x轴;
(3)当 ,b满足什么条件时,
,b满足什么条件时, 在
在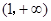 上恒取正值.
上恒取正值.
(本小题满分10分)选修4-1《几何证明选讲》.
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点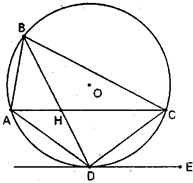
(Ⅰ)求证:BD平分∠ABC
(Ⅱ)若AB=4,AD=6,BD=8,求AH的长.
(本小题满分12分)
已知函数f(x)= -x (e为自然对数的底数).
-x (e为自然对数的底数).
(Ⅰ)求f(x)的最小值;
(Ⅱ)不等式f(x)>ax的解集为P,若M={x| ≤x≤2}且M∩P≠
≤x≤2}且M∩P≠ ,求实数a的
,求实数a的
取值范围;
(Ⅲ)已知n∈N﹡,且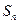 =
=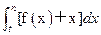 (t为常数,t≥0),是否存在等比数列{
(t为常数,t≥0),是否存在等比数列{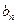 },使得b1+b2+…
},使得b1+b2+…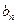 =
=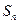 ?若存在,请求出数列{
?若存在,请求出数列{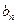 }的通项公式;若不存在,请说明理由.
}的通项公式;若不存在,请说明理由.
(本小题满分12分)
已知椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为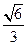 ,其左、右焦点分别是F1、F2,点P是坐标平面内的一点,且|OP|=
,其左、右焦点分别是F1、F2,点P是坐标平面内的一点,且|OP|= ,
,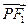 ·
·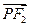 =
= (点O为坐标原点).
(点O为坐标原点).
(Ⅰ)求椭圆C的方程;
(Ⅱ)直线y=x与椭圆C在第一象限交于A点,若椭圆C上两点M、N使 +
+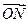 =
=
λ ,λ∈(0,2)求△OMN面积的最大值.
,λ∈(0,2)求△OMN面积的最大值.
(本小题满分12分)
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=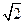 .
.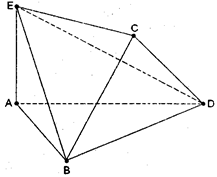
(Ⅰ)求证:DE⊥AC;
(Ⅱ)求DE与平面BEC所成角的正弦值;
(Ⅲ)直线BE上是否存在一点M,使得CM∥平面ADE,若存在,求点M的位置,不存在请说明理由.
(本小题满分12分)
某班主任为了解所带班学生的数学学习情况,从全班学生中随机抽取了20名学生,对他们的数学成绩进行统计,统计结果如图.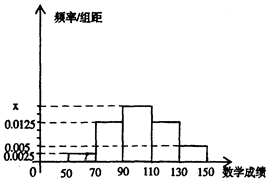
 (Ⅰ)求x的值和数学成绩在110分以上的人数;
(Ⅰ)求x的值和数学成绩在110分以上的人数;
(Ⅱ)从数学成绩在110分以上的学生中任意抽 取3人,成绩在130分以上的人数为ξ,求ξ的期望.
取3人,成绩在130分以上的人数为ξ,求ξ的期望.