惠州市在每年的春节后，市政府都会发动公务员参与到植树活动中去．林管部门在植树前，为保证树苗的质量，都会在植树前对树苗进行检测．现从甲乙两种树苗中各抽测了10株树苗的高度，量出的高度如下(单位：厘米)
甲：37,21,31,20,29,19,32,23,25,33
乙：10,30,47,27,46,14,26,10,44,46
（1）根据抽测结果，完成答题卷中的茎叶图，并根据你填写的茎叶图，对甲、乙两种树苗的高度作比较，写出两个统计结论；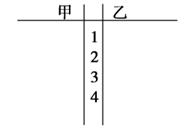
（2）设抽测的10株甲种树苗高度平均值为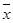
，将这10株树苗的高度依次输入如图程序框图进行运算，问输出的S大小为多少？并说明S的统计学意义．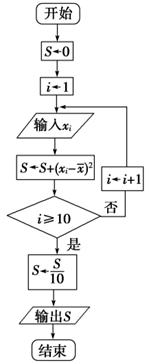
(本小题满分12分)已知条件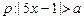
，（
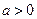）和条件
，
请选取适当的实数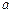
的一个值，使命题：“
”为真命题，它的逆命题为假命题，并说明理由。
在平面直角坐标系xOy中，已知圆C1：(x＋3)2＋(y－1)2＝4和圆C2：(x
－4)2＋(y－5)2＝4.
（1）若点M∈⊙ C1, 点N∈⊙C2,求|MN|的取值范围；
(2)若直线l过点A(4,0)，且被圆C1截得的弦长为2 
，求直线l的方程；
(3)设P为平面上的点，满足：存在过点P的无数多对互相垂直的直线l1和l2，它们分别与圆C1和圆C2相交，且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等，试求所有满足条件的点P的坐标。
如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，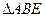
是等腰直角三角形，AB=AE，FA=FE，
∠AEF=45°
（1）求证：EF⊥平面BCE；
（2）设线段CD的中点为P，在直线AE上是否存在一点M，使得PM//平面BCE？若存在，请指出点M的位置，并证明你的结论；若不存在，请说明理由。
已知点P到两个定点M(－1,0)，
N(1,0)的距离的比为。
（1）求证点P在一定圆上，并求此圆圆心和半径；
（2）若点N到直线PM的距离为1，求直线PN的方程。
设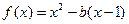
（1）若对任意的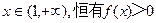
成立，求实数b的取值范围；
（2）若存在
成立，
求实数b的取值范围。