如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象（分别为正比例函数和一次函数）.两地间的距离是80千米.请你根据图象回答或解决下面的问题：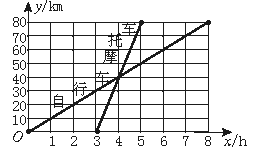
（1）谁出发的较早？早多长时间？谁到达乙地较早？早到多长时间？
（2）两人在途中行驶的速度分别是多少？
（3）请你分别求出表示自行车和摩托车行驶过程的函数解析式（不要求写出自变量的取值范围）；
（4）指出在什么时间段内两车均行驶在途中（不包括端点）；在这一时间段内，请你分别按下列条件列出关于时间x的方程或不等式（不要化简，也不要求解）：①自行车行驶在摩托车前面；②自行车与摩托车相遇；③自行车行驶在摩托车后面.
（1）解不等式：2x－1＜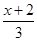
；（2）解方程组：
.
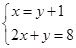（1）计算：tan45º－(－2)2－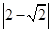
；
（2）已知x2－4x－1=0，求代数式(2x－3)2－(x＋y)(x－y)－y2的值
阅读下列材料：
一般地，n个相同的因数a相乘
记为an，记为an．如2×2×2=23=8，此时，3叫做以2为底8的对数，记为log28（即log28=3）．一般地，若an=b（a＞0且a≠1，b＞0），则n叫做以a为底b的对数，记为logab（即logab=n）．如34=81，则4叫做以3为底81的对数，记为log381（即log381=4）．
（1）计算以下各对数的值：
log24=，log216=，log264=．
（2）观察（1）中三数4、16、64之间满足怎样的关系式，log24、log216、log264之间又满足怎样的关系式。
（3）由（2）的结果，你能归纳出一个一般性的结论吗？
logaM+logaN=；（a＞0且a≠1，M＞0，N＞0）
（4）根据幂的运算法则：an•am=an+m以及对数的含义证明上述结论．
如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．
（1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．(提示：过点P作PE∥l1)
（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？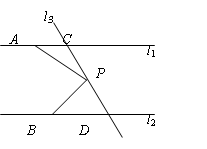
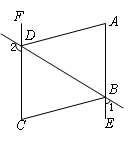
如图，已知∠1＋∠2=180º，∠DAE=∠BCF．
（1）试判断直线AE与CF有怎样的位置关系？并说明理由；
（2）若∠BCF=70º，求∠ADF的度数；