求满足 的最大整数
的最大整数 .
.
如图,四棱锥P—ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点.
(1)求证:BE//平面PAD;
(2)若BE⊥平面PCD。
(i)求异面直线PD与BC所成角的余弦值;
(ii)求二面角E—BD—C的余弦值.
数列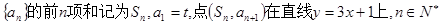 .
.
(1)
(2)在(1)的结论下,设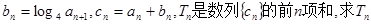
已知向量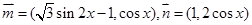 ,设函数
,设函数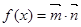 。
。
(1)求函数 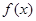 的最小正周期及
的最小正周期及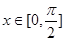 时的最大值;
时的最大值;
(2)把函数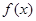 的图象向左平移
的图象向左平移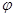
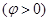 个单位,所得到的图象对应的函数为奇函数,求
个单位,所得到的图象对应的函数为奇函数,求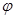 的最小值。
的最小值。
(本小题满分12分)已知函数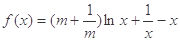 ,其中常数
,其中常数 .
.
(1)当 时,求函数
时,求函数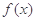 的极大值;
的极大值;
(2)当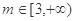 时,曲线
时,曲线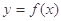 上总存在相异两点
上总存在相异两点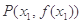 ,
,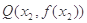 ,使得曲线
,使得曲线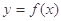 在点
在点 处的切线互相平行,求
处的切线互相平行,求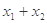 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆C的对称中心为原点O,焦点在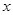 轴上,左右焦点分别为
轴上,左右焦点分别为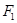 和
和 ,且
,且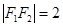 ,点
,点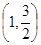 在该椭圆上.
在该椭圆上.
(1)求椭圆C的方程;
(2)过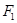 的直线
的直线 与椭圆C相交于
与椭圆C相交于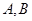 两点,若
两点,若 的面积为
的面积为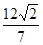 ,求以
,求以 为圆心且与直线
为圆心且与直线 相切圆的方程.
相切圆的方程.