甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为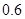
，被甲或乙解出的概率为
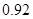，（1）求该题被乙独立解出的概率；（2）求解出该题的人数
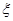的数学期望和方差
（本小题满分16分）已知: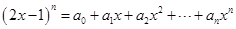
（
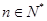,n为常数）．
（1）求
；
（2）我们知道二项式
的展开式
．若该等式两边对x求导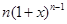得：
=
,令x=1，可得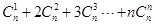
=
．利用此方法解答以下问题：
①求
；
②求
．
（本小题满分16分）袋中有大小相同的三个球，编号分别为1,2,3．从袋中每次取出一个球，若取到的球的编号为2，则把该球编号记下再把编号数改为1后放回袋中继续取球；若取到球的编号为奇数，则取球停止，取球停止后用X表示“所有被取球的编号之和”。
（1）求X的概率分布；
（2）求X的数学期望及方差．
（本小题满分14分）已知
的展开式中，各项系数和比它的二项式系数和大992，
（1）求n值；
（2）求展开式中系数最大项。
（本小题满分14分）将四个编号为1,2,3,4的相同小球放入编号为1,2,3,4的四个盒子中，
（1）若每个盒子放一个小球，求有多少种放法;
（2）若每个盒子放一球，求恰有1个盒子的号码与小球的号码相同的放法种数；
（3）求恰有一个空盒子的放法种数。
（本小题满分14分）已知函数
．
（1）若函数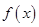
在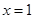
处的切线的斜率为3，求
的值；
（2）若函数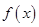在区间[1,2]上为增函数，求的取值范围。