(本小题满分14分)
命题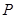 :函数
:函数 在
在 上是增函数;命题
上是增函数;命题 :
: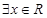 ,使得
,使得 .
.
(1)若命题“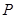 且
且 ”为真,求实数
”为真,求实数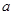 的取值范围;
的取值范围;
(2)若命题“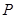 或
或 ”为真,“
”为真,“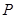 且
且 ”为假,求实数
”为假,求实数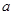 的取值范围.
的取值范围.
在极坐标系中,圆C的方程为ρ=2 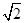 sin
sin 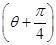 ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为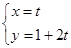 (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系.
在平面直角坐标系xOy中,直线x+y+2=0在矩阵M=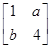 对应的变换作用下得到直线m:x-y-4=0,求实数a,b的值.
对应的变换作用下得到直线m:x-y-4=0,求实数a,b的值.
求矩阵 的特征值及对应的特征向量.
的特征值及对应的特征向量.
如图,圆O的直径AB=4,C为圆周上一点,BC=2,过C作圆O的切线l,过A作l的垂线AD,AD分别与直线l、圆O交于点D,E,求线段AE的长.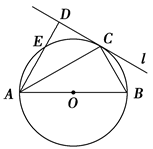
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证:
(1)∠AED=∠AFD;
(2)AB2=BE·BD-AE·AC.