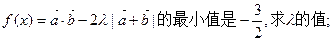已知函数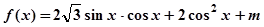 在区间
在区间 上的最大值为2
上的最大值为2 .
.
(1)求常数 的值;
的值;
(2)在 中,角
中,角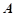 ,
, ,
, 所对的边是
所对的边是 ,
,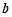 ,
, ,若
,若 ,
, ,
, 面积为
面积为 . 求边长
. 求边长 .
.
某种植企业同时培育甲、乙两个品种杉树幼苗,甲品种杉树幼苗培育成功则每株利润80元,培育失败,则每株亏损20元;乙品种杉树幼苗培育成功则每株获利润150元,培育失败,则每株亏损50元。统计数据表明:甲品种杉树幼苗培育成功率为90%,乙品种杉树幼苗培育成功率为80%。假设每株幼苗是否培育成功相互独立。
(I)求培育3株甲品种杉树幼苗成功2株的概率;
(II)记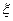 为培育1株甲品种杉树幼苗与1株乙品种杉树幼苗可获得的总利润,求
为培育1株甲品种杉树幼苗与1株乙品种杉树幼苗可获得的总利润,求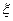 的分布列及其期望。
的分布列及其期望。
已知直线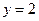 与函数
与函数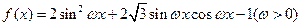 的图像的两个相邻交点之间的距离为
的图像的两个相邻交点之间的距离为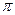 。
。
(I)求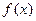 的解析式,并求出
的解析式,并求出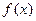 的单调递增区间
的单调递增区间
(II)将函数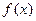 的图像向左平移
的图像向左平移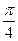 个单位得到函数
个单位得到函数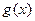 的图像,求函数
的图像,求函数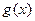 的最大值及
的最大值及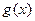 取得最大值时x的取值集合。
取得最大值时x的取值集合。

在编号1~9的九个盒子中,共 放有351粒
放有351粒 米,己知每个盒子都比前一号盒子多放同样粒数的米
米,己知每个盒子都比前一号盒子多放同样粒数的米 。
。
(1)如果1 号盒子内放了11粒米,那么后面的盒子比它前一号的盒子多放几粒米?
号盒子内放了11粒米,那么后面的盒子比它前一号的盒子多放几粒米?
(2)如果3号盒子内放了23粒米,那么后面的盒子比它前一号的盒子多放几粒米?
已知向量
⑴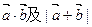 ;
;
⑵若