设 为实数,函数
为实数,函数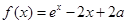 ,
, .
.
(1)求 的单调区间与极值;
的单调区间与极值;
(2)求证:当 且
且 时,
时, .
.
已知f(x)=x+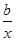 -3,x∈[1,2].
-3,x∈[1,2].
(1)当b=2时,求f(x)的值域;
(2)若b为正实数,f(x)的最大值为M,最小值为m,且满足M-m≥4,求b的取值范围.
已知A={x|ax-1>0},B={x|x2-3x+2>0}.
(1)若A∩B=A,求实数a的取值范围;
(2)若A∩∁RB≠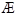 ,求实数a的取值范围.
,求实数a的取值范围.
设关于x的不等式x(x-a-1)<0(a∈R)的解集为M,不等式x2-2x-3≤0的解集为N.
(1)当a=1时,求集合M;
(2)若M∪N=N,求实数a的取值范围.
若全集U={1,2,3,4,5,6},M∩N=N,N={1,4},试求满足条件的集合M的个数.
已知A={a+2,(a+1)2,a2+3a+3}且1∈A,求实数a的值.