空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
| PM2.5日均浓度 |
0~35 |
35~75 |
75~115 |
115~150 |
150~250 |
>250 |
| 空气质量级别 |
一级 |
二级 |
三级 |
四级 |
五级 |
六级 |
| 空气质量类别 |
优 |
良 |
轻度污染 |
中度污染 |
重度污染 |
严重污染 |
某市2012年3月8日—4月7日(30天)对空气质量指数PM2.5进行监测,获得数据后整理得到如下条形图: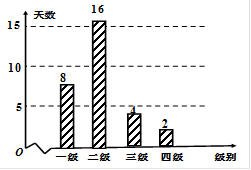
(1)估计该城市一个月内空气质量类别为良的概率;
(2)从空气质量级别为三级和四级的数据中任取2个,求至少有1天空气质量类别为中度污染的概率。
已知函数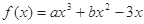 在
在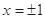 处取得极值.
处取得极值.
(1)讨论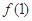 和
和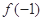 是函数
是函数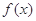 的极大值还是极小值;
的极大值还是极小值;
(2)过点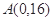 作曲线
作曲线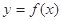 的切线,求此切线方程.
的切线,求此切线方程.
已知函数 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M 处的切线方程为
处的切线方程为 .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 的单调区间.
的单调区间.
已知函数 ,若存在
,若存在 ,使
,使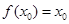 ,则称
,则称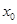 是函数
是函数 的一个不动点.设二次函数
的一个不动点.设二次函数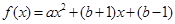 .
.
(1)对任意实数 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求 的取值范围;
的取值范围;
(2)在(1)的条件下,若 的图象上
的图象上 两点的横坐标是
两点的横坐标是 的不动点,且
的不动点,且 两点关于直线
两点关于直线 对称,求
对称,求 的最小值.
的最小值.
已知向量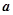
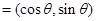 ,
,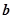
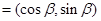 ,且
,且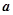 与
与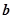 满足
满足 ,其中实数
,其中实数 .
.
(1)试用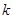 表示
表示 ;
;
(2)求 的最小值,并求此时
的最小值,并求此时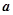 与
与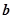 的夹角
的夹角 的值.
的值.
设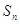 为数列{
为数列{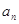 }的前项和,已知
}的前项和,已知 ,2
,2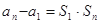 ,
, N
N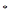
(1)求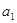 ,并求数列{
,并求数列{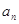 }的通项公式;(2)求数列{
}的通项公式;(2)求数列{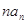 }的前
}的前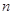 项和.
项和.