在平面直角坐标系xOy中,点P是圆 上一动点,
上一动点, x轴于点D.记满足
x轴于点D.记满足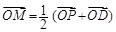 的动点M的轨迹为Γ.
的动点M的轨迹为Γ.
(1)求轨迹Γ的方程;
(2)已知直线 与轨迹Γ交于不同两点A,B,点G是线段AB中点,射线OG交轨迹Γ于点Q,且
与轨迹Γ交于不同两点A,B,点G是线段AB中点,射线OG交轨迹Γ于点Q,且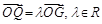 .
.
①证明:
②求△AOB的面积S(λ)的解析式,并计算S(λ)的最大值.
如图,已知 的直径AB=3,点C为
的直径AB=3,点C为 上异于A,B的一点,
上异于A,B的一点, 平面ABC,且VC=2,点M为线段VB的中点.
平面ABC,且VC=2,点M为线段VB的中点.
(1)求证: 平面VAC;
平面VAC;
(2)若AC=1,求二面角M-VA-C的余弦值.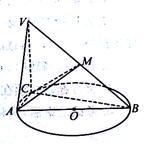
某地区为了解高二学生作业量和玩电脑游戏的情况,对该地区内所有高二学生采用随机抽样的方法,得到一个容量为200的样本.统计数据如下:
(1)已知该地区共有高二学生42500名,根据该样本估计总体,其中喜欢电脑游戏并认为作业不多的人有多少名?
(2)在A,B,C,D,E,F六名学生中,仅有A,B两名学生认为作业多.如果从这六名学生中随机抽取两名,求至少有一名学生认为作业多的概率.
在△ABC中,角A,B,C所对的边分别为a,b,c,已知向量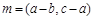 ,
, ,且
,且
(1)求角B的大小;
(2)求函数 的值域.
的值域.
已知等差数列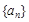 的前n项和为
的前n项和为 ,且
,且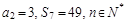
(1)求数列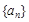 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列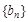 的前n项和Tn.
的前n项和Tn.