(本小题满分14分)已知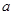 为实数,
为实数,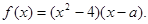
(1)若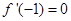 ,求
,求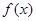 在
在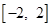 上最大值和最小值;
上最大值和最小值;
(2)若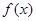 在
在 和
和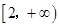 上都是递增的,求
上都是递增的,求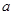 的取值范围。
的取值范围。
已知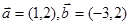 ,当
,当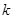 为何值时,
为何值时,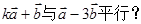
平行时它们是同向还是反向?
(本题满分9分)
已知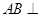 平面
平面 ,
,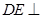 平面
平面 ,△
,△ 为等边三角形,
为等边三角形,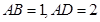 ,
,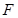 为
为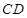 的中点且
的中点且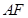 ∥平面
∥平面 .
.
(I) 求线段 的长;
的长;
(II) 求直线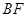 和平面
和平面 所成角的正切值.
所成角的正切值.
(本题满分8分)
已知圆 与直线
与直线 相交于
相交于 两点.
两点.
(Ⅰ)求弦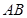 的长;
的长;
(Ⅱ)若圆 经过
经过 ,且圆
,且圆 与圆
与圆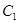 的公共弦平行于直线
的公共弦平行于直线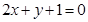 ,求圆
,求圆 的方程.
的方程.
.(本题满分7分)
已知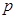 :过点
:过点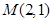 的直线与焦点在
的直线与焦点在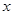 轴上的椭圆
轴上的椭圆 恒有公共点,
恒有公共点, :方程
:方程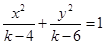 表示双曲线,问:
表示双曲线,问: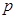 是
是 的什么条件?并说明理由.
的什么条件?并说明理由.
(本题满分6分)
已知圆锥的正视图是边长为2的正三角形,O是底面圆心.
(Ⅰ)求圆锥的侧面积;
(Ⅱ)经过圆锥的高AO的中点O¢作平行于圆锥底面的截面,
求截得的两部分几何体的体积比.