（本小题满分12分）椭圆
：
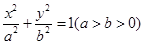的左、右焦点分别为
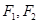，焦距为2，，过
作垂直于椭圆长轴的弦长
为3．
(Ⅰ)
求椭圆的方程；
（Ⅱ）若过的直线l交椭圆于
两点．并判断是否存在直线l使得
的夹角为钝角，若存在，求出l的斜率k的取值范围。
已知ABCD－A′B′C′D′是平行六面体．
(1)化简＋＋，并在图形中标出其结果；
(2)设M是底面ABCD的中心，N是侧面BCC′B′的对角线BC′上的点，且BN∶NC′＝3∶1，设＝α＋β＋γ，试求α，β，γ之值．
试用向量证明三垂线定理及其逆定理．
如右图
，A、B、C、D为空间四点．在△ABC中，AB＝2，AC＝BC＝.等边三角形ADB以AB为轴运动．
(1)当平面ADB⊥平面ABC时，求CD；
(2)当△ADB转动时，是否总有AB⊥CD?
证明你的结论．
如右图所示，四棱锥P－ABCD的底面是边长为1的正方形，PA⊥CD，PA＝1，PD＝.
(1)求证：PA⊥平面ABCD；
(2)求四棱锥P－ABCD的体积
如右图所示，在四棱锥P—ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA＝AB＝1，AD＝，点F是PB的中点，点E在边BC上移动．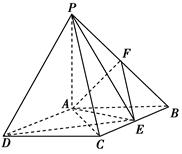
(1)求三棱锥E—PAD的体积；
(2)当点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
(3)证明：无论点E在边BC的何处，都有PE⊥AF.