(本小题满分12分)
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组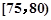 ,第2组
,第2组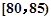 ,第3组
,第3组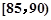 ,第4组
,第4组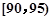 ,第5组
,第5组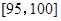 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.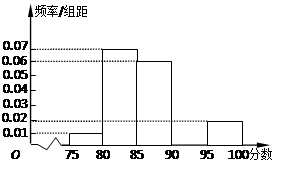
(1)求出第4组的频率;
(2)如果用分层抽样的方法从“优秀”和“良好” 的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(本小题15分)已知 ,
, 是实数,方程
是实数,方程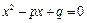 有两个实根
有两个实根 ,
, ,数列
,数列 满足
满足 ,
, ,
,
(Ⅰ)求数列 的通项公式(用
的通项公式(用 ,
, 表示);
表示);
(Ⅱ)若 ,
, ,求
,求 的前
的前 项和.
项和.
(本小题满分14分)设直线 (其中
(其中 ,
, 为整数)与椭圆
为整数)与椭圆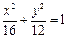 交于不同两点
交于不同两点 ,
, ,与双曲线
,与双曲线 交于不同两点
交于不同两点 ,
, ,问是否存在直线
,问是否存在直线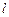 ,使得向量
,使得向量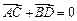 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
(本小题满分14分)已知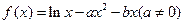 .
.
(1)若 ,函数
,函数 在其定义域内是增函数,求
在其定义域内是增函数,求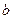 的取值范围.
的取值范围.
(2)在(1)的结论下,设 ,求函数
,求函数 的最小值;
的最小值;
(3)若 的图象与
的图象与 轴交于
轴交于 ,
, 中点为
中点为 ,求证:
,求证: .
.
(本小题满分13分)直线 与椭圆
与椭圆 交于
交于 ,
, 两点,已知
两点,已知 ,
, ,若
,若 且椭圆的离心率
且椭圆的离心率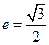 ,又椭圆经过点
,又椭圆经过点 ,
, 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线 过椭圆的焦点
过椭圆的焦点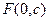 ,(
,( 为半焦距),求直线
为半焦距),求直线 的斜率
的斜率 的值;
的值;
(Ⅲ)试问: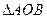 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
(本小题满分13分)已知数列 的前
的前 项和为
项和为 ,数列
,数列 满足
满足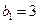 ,
, .
.
(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列 的前
的前 项和
项和 ;
;
(3)是否存在非零实数 ,使得数列
,使得数列 为等差数列,证明你的结论.
为等差数列,证明你的结论.