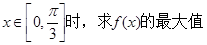给定椭圆 :
: ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 的“准圆”。若椭圆
的“准圆”。若椭圆 的一个焦点为
的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为 .
.
(Ⅰ)求椭圆 的方程和其“准圆”方程.
的方程和其“准圆”方程.
(Ⅱ)点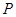 是椭圆
是椭圆 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点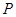 作直线
作直线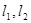 使得
使得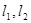 与椭圆
与椭圆 都只有一个交点,且
都只有一个交点,且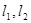 分别交其“准圆”于点
分别交其“准圆”于点 ,求证:
,求证: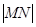 为定值.
为定值.
设椭圆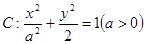 的左、右顶点分别为
的左、右顶点分别为 、
、 ,点
,点 在椭圆上且异于
在椭圆上且异于 、
、 两点,
两点,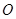 为坐标原点.
为坐标原点.
(1)若直线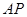 与
与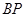 的斜率之积为
的斜率之积为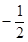 ,求椭圆的离心率;
,求椭圆的离心率;
(2)对于由(1)得到的椭圆 ,过点
,过点 的直线
的直线 交
交 轴于点
轴于点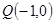 ,交
,交 轴于点
轴于点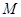 ,若
,若 ,求直线
,求直线 的斜率.
的斜率.
已知函数
(1)若 ,求
,求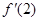 的值;
的值;
(2)若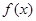 的图像与直线
的图像与直线 相切于点
相切于点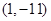 ,求
,求 的值;
的值;
(3)在(2)的条件下,求函数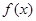 的单调区间.
的单调区间.
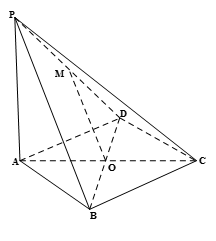
如图 ,在四棱锥
,在四棱锥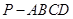 中,
中,
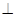 平面
平面 ,底面
,底面 是菱形,点O是对角线
是菱形,点O是对角线 与
与 的交点,
的交点, 是
是 的中点,
的中点, .
.
(1) 求证: 平面
平面 ;
;
(2) 平面
 平面
平面 ;
;
(3) 当四棱锥 的体积等于
的体积等于 时,求
时,求 的长.
的长.
某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了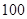 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:
| 数学 |
语文 |
总计 |
|
| 初中 |
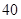 |
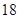 |
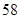 |
| 高中 |
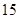 |
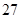 |
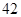 |
| 总计 |
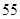 |
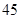 |
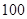 |
(1) 用分层抽样的方法从喜欢语文的学生中随机抽取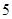 名,高中学生应该抽取几名?
名,高中学生应该抽取几名?
(2) 在(1)中抽取的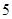 名学生中任取
名学生中任取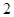 名,求恰有
名,求恰有 名初中学生的概率.
名初中学生的概率.
设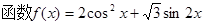
(1)求函数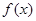 的最小正周期和单调递增区间
的最小正周期和单调递增区间
(2)当