(本题12分)解不等式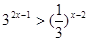 .
.
(本小题满分14分)
某商品近一个月内(30天)预计日销量y=f(t)(件)与时间t(天)的关系如图1所示,单价y=g(t)(万元/件)与时间t(天)的函数关系如图2所示,(t为整数)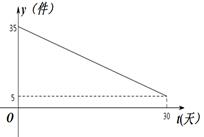

图1图2
(1)试写出f(t)与g(t)的解析式;(6分)
(2)求此商品日销售额的最大值?(8分)
(本小题满分12分)
函数 的定义域为[-1,2],
的定义域为[-1,2],
(1)若 ,求函数
,求函数 的值域;
的值域;
(2)若 为非负常数,且函数
为非负常数,且函数 是[-1,2]上的单调函数,求
是[-1,2]上的单调函数,求 的范围及函数
的范围及函数 的值域。
的值域。
(本小题满分14分)
函数 和
和 的图像的示意图如图所示, 两函数的图像在第一象限只有两个交点
的图像的示意图如图所示, 两函数的图像在第一象限只有两个交点 ,
, ,
,
(1)请指出示意图中曲线 ,
, 分别对应哪一个函数;
分别对应哪一个函数;
(2)比较 的大小,并按从小到大的顺序排列;
的大小,并按从小到大的顺序排列;
(3)设函数 ,则函数
,则函数 的两个零点为
的两个零点为 ,如果
,如果 ,
, ,其中
,其中 为整数,指出
为整数,指出 ,
, 的值,并说明理由;
的值,并说明理由;
(本小题满分14分)
已知集合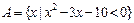 ,
, ,
,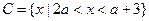 .若
.若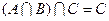 ,试确定实数
,试确定实数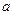 的取值范围.
的取值范围.
(本小题满分12分)
计算下列各式的值:
(1)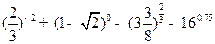 ; (2)
; (2) 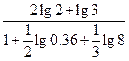 ;
;