(本小题满分 分)设函数
分)设函数 的最高点
的最高点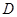 的坐标为(
的坐标为( ),由最高点
),由最高点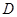 运动到相邻最低点时,函数图形与
运动到相邻最低点时,函数图形与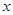 的交点的坐标为(
的交点的坐标为( ).
).
(1)求函数 的解析式.
的解析式.
(2)当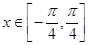 时,求函数
时,求函数 的最大值和最小值以及分别取得最大值和最小值时
的最大值和最小值以及分别取得最大值和最小值时
相应的自变量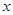 的值.
的值.
(3)将函数 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 的单调减区间.
的单调减区间.
设曲线 在矩阵 对应的变换作用下得到的曲线为 .
(Ⅰ)求实数
的值
(Ⅱ)求
的逆矩阵
已知函数
.
(Ⅰ)若曲线
在点
处的切线平行于
轴,求函数
的单调区间;
(Ⅱ)试确定
的取值范围,使得曲线
上存在唯一的点
,曲线在该点处的切线与曲线只有一个公共点
.
如图,椭圆
:
的左焦点为
,右焦点为
,离心率
。过
的直线交椭圆于
两点,且
的周长为8
(Ⅰ)求椭圆
的方程。
(Ⅱ)设动直线
:
与椭圆
有且只有一个公共点
,且与直线
相较于点
。试探究:在坐标平面内是否存在定点
,使得以
为直径的圆恒过点
?若存在,求出点
的坐标;若不存在,说明理由
如图,在长方体 中 , 为 中点.
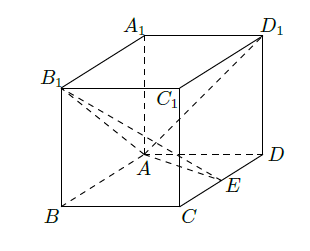
(Ⅰ)求证:
;
(Ⅱ)在棱
上是否存在一点
,使得
平面
?若存在,求
的长;若不存在,说明理由.
(Ⅲ)若二面角
的大小为
,求
的长.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数。
(1)
(2)
(3)
(4)
(5)
(Ⅰ)试从上述五个式子中选择一个,求出这个常数.
(Ⅱ)根据(Ⅰ)的计算结果,将该同学的发现推广位三角恒等式,并证明你的结论.