如图,在某建筑物AC上,挂着“魅力湖州”的宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为 ,再往条幅方向前行20米到达点E处,看到条幅顶端B,测得仰角为
,再往条幅方向前行20米到达点E处,看到条幅顶端B,测得仰角为 ,求宣传条幅BC的长(小明的身高不计)。
,求宣传条幅BC的长(小明的身高不计)。
要了解某地区九年级学生的身高情况,从中随机抽取150名学生的身高作为一个样本,身高均在141cm~175cm之间(取整数厘米),整理后分成7组,绘制出频数分布直方图(不完整).根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)该地区共有3000名九年级学生,估计其中身高不低于161cm的人数;
(3)估计该地区九年级学生身高不低于151cm的概率.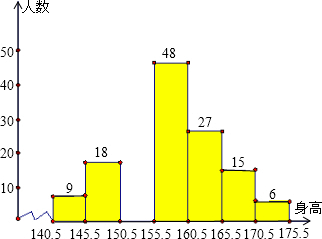
某校学生会准备调查六年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
(1)确定调查方式时,甲同学说:“我到六年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到六年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
| 类别 |
频率(人数) |
频率 |
| 武术类 |
0.25 |
|
| 书画类 |
20 |
0.2 |
| 棋牌类 |
15 |
b |
| 器乐类 |
||
| 合计 |
a |
1 |
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.
请你根据以上图表提供的信息解答下列问题:
①a=,b=;
②在扇形统计图中,器乐类所对应扇形的圆心角的度数是;
③若该校六年级有学生560人,请你估计大约有多少学生参加武术类校本课程.
水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为 米,加固后大坝的横截面积为梯形ABED,CE的长为8米.
米,加固后大坝的横截面积为梯形ABED,CE的长为8米.
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?
(2)求加固后的大坝背水坡面DE的坡度.
如图,一艘货轮在A处发现其北偏东45°方向有一海盗船,立即向位于正东方向B处的海警舰发出求救信号,并向海警舰靠拢,海警舰立即沿正西方向对货轮实施救援,此时距货轮200海里,并测得海盗船位于海警舰北偏西60°方向的C处.
(1)求海盗船所在C处距货轮航线AB的距离.
(2)若货轮以45海里/时的速度在A处沿正东方向海警舰靠拢,海盗以50海里/时的速度由C处沿正南方向对货轮进行拦截,问海警舰的速度应为多少时才能抢在海盗之前去救货轮?(结果保留根号)
如图,小明想用所学的知识来测量湖心岛上的迎宾槐与湖岸上凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东45°方向(点A、B、C在同一平面上),请你利用小明测得的相关数据,求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离(结果精确到1米).(参考数据sin25°≈0.4226,cos25°≈0.9063,tan25°≈0.4663,sin65°≈0.5563,cos65°≈0.4226,tan65°≈2.1445)