如图①,一条笔直的公路上有A、B、C 三地,B、C 两地相距 150 千米,甲、乙两辆汽车分别从B、C 两地同时出发,沿公路匀速相向而行,分别驶往C、B 两地.甲、乙两车到A 地的距离 、
、 (千米)与行驶时间 x(时)的关系如图②所示.
(千米)与行驶时间 x(时)的关系如图②所示. 
根据图象进行以下探究:
(1)请在图①中标出 A地的位置,并作简要的文字说明;
(2)求图②中M点的坐标,并解释该点的实际意义;
(3)在图②中补全甲车的函数图象,求甲车到 A地的距离 与行驶时间x的函数关系式;
与行驶时间x的函数关系式;
(4)A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.
如图,抛物线 与 轴交于 , 两点(点 在点 左侧),与 轴交于点 ,点 是抛物线上的一个动点,且位于第四象限,连接 、 、 、 ,延长 交 轴于点 .
(1)若 为等腰直角三角形,求 的值;
(2)若对任意 , 、 两点总关于原点对称,求点 的坐标(用含 的式子表示);
(3)当点 运动到某一位置时,恰好使得 ,且点 为线段 的中点,此时对于该抛物线上任意一点 , 总有 成立,求实数 的最小值.

若三个非零实数 , , 满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数 , , 构成“和谐三组数”.
(1)实数1,2,3可以构成“和谐三组数”吗?请说明理由;
(2)若 , , 三点均在函数 为常数, 的图象上,且这三点的纵坐标 , , 构成“和谐三组数”,求实数 的值;
(3)若直线 与 轴交于点 , ,与抛物线 交于 , , , 两点.
①求证: , , 三点的横坐标 , , 构成“和谐三组数”;
②若 , ,求点 , 与原点 的距离 的取值范围.
自从湖南与欧洲的“湘欧快线”开通后,我省与欧洲各国经贸往来日益频繁,某欧洲客商准备在湖南采购一批特色商品,经调查,用16000元采购 型商品的件数是用7500元采购 型商品的件数的2倍,一件 型商品的进价比一件 型商品的进价多10元.
(1)求一件 , 型商品的进价分别为多少元?
(2)若该欧洲客商购进 , 型商品共250件进行试销,其中 型商品的件数不大于 型的件数,且不小于80件.已知 型商品的售价为240元 件, 型商品的售价为220元 件,且全部售出.设购进 型商品 件,求该客商销售这批商品的利润 与 之间的函数关系式,并写出 的取值范围;
(3)在(2)的条件下,欧洲客商决定在试销活动中每售出一件 型商品,就从一件 型商品的利润中捐献慈善资金 元,求该客商售完所有商品并捐献慈善资金后获得的最大收益.
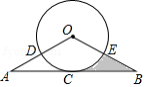
如图, 与 相切于点 , , 分别交 于点 , ,
(1)求证: ;
(2)已知 , ,求阴影部分的面积.
为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在 处测得灯塔 在北偏东 方向上,继续航行1小时到达 处,此时测得灯塔 在北偏东 方向上.
(1)求 的度数;
(2)已知在灯塔 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
