某产品按行业生产标准分成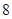个等级，等级系数依次为，其中为标准，-优题课

题文

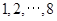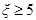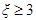某产品按行业生产标准分成个等级，等级系数依次为，其中为标准，为标准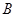，产品的等级系数越大表明产品的质量越好，已知某厂执行标准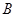生产该产品，且该厂的产品都符合相应的执行标准.
（Ⅰ）从该厂生产的产品中随机抽取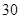件，相应的等级系数组成一个样本，数据如下：
3   5   3   3   8   5   5   6   3   4
6   3   4   7   5   3   4   8   5   3
8   3   4   3   4   4   7   5   6   7
该行业规定产品的等级系数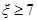的为一等品，等级系数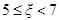的为二等品，等级系数的为三等品，
（1）试分别估计该厂生产的产品的一等品率、二等品率和三等品率；
（2）已知该厂生产一件该产品的利润y（单位：元）与产品的等级系数的关系式为：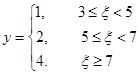
，从该厂生产的产品中任取一件，其利润记为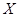，用这个样本的频率分布估计总体分布，将频率视为概率，求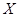的分布列和数学期望．

科目数学题型解答题难度较易

知识点：随机思想的发展

登录免费查看答案和解析

相关试题

某实验室一天的温度（单位： $^{°} C$ ）随时间 $t$ （单位： $h$ ）的变化近似满足函数关系；
$f (t) = 10 - \sqrt{3} \cos \frac{π}{12} t - \sin \frac{π}{12} t, t \in [0, 24]$ .
（1）求实验室这一天的最大温差；
（2）若要求实验室温度不高于11 $^{°} C$ ，则在哪段时间实验室需要降温？

设 $f (x)$ 是定义在 $(0, + \infty)$ 上的函数，且 $f (x) > 0$ ，对任意 $a > 0, b > 0$ ，若经过点 $(a, f (a))$ ， $(b, - f (b))$ 的直线与 $x$ 轴的交点为 $(c, 0)$ ，则称 $c$ 为 $a, b$ 关于函数 $f (x)$ 的平均数，记为 $M_{f} (a, b)$ ，例如，当 $f (x) = 1 (x > 0)$ 时，可得 $M_{f} (a, b) = c = \frac{a + b}{2}$ ，即 $M_{f} (a, b)$ 为 $a, b$ 的算术平均数.
当 $f (x) =$ ( $x > 0$ )时， $M_{f} (a, b)$ 为 $a, b$ 的几何平均数；
当 $f (x) =$ ( $x > 0$ )时， $M_{f} (a, b)$ 为 $a, b$ 的调和平均数 $\frac{2 a b}{a + b}$ ；
（以上两空各只需写出一个符合要求的函数即可）

函数 $f (x) = \ln (x + 1) - \frac{a x}{x + a} (a > 1)$ .
（1）讨论 $f (x)$ 的单调性；
（2）设 $a_{1} = 1, a_{n + 1} = \ln (a_{n} + 1)$ ，证明： $\frac{2}{n + 2} < a_{n} < \frac{3}{n + 2}$ .

已知抛物线 $C :$ $x + y - 1 = 0$ $y^{2} = 2 p x (p > 0)$ 的焦点为 $F$ ，直线 $y = 4$ 与 $y$ 轴的交点为 $P$ ，与 $C$ 的交点为 $Q$ ，且 $|Q F| = \frac{5}{4} |F Q|$ .
（1）求 $C$ 的方程；
（2）过 $F$ 的直线 $l$ 与 $C$ 相交于 $A, B$ 两点，若 $A B$ 的垂直平分线 $l `$ 与 $C$ 相较于 $M, N$ 两点，且 $A, M, B, N$ 四点在同一圆上，求 $l$ 的方程.

设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为 $0.6, 0.5, 0.5, 0.4$ 各人是否需使用设备相互独立.
（1）求同一工作日至少3人需使用设备的概率；
（2） $X$ 表示同一工作日需使用设备的人数，求 $X$ 的数学期望.

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号