(满分12分)
某市居民生活用水标准如下：
| 用水量t（单位：吨） |
每吨收费标准（单位：元） |
| 不超过2吨部分 |
m |
| 超过2吨不超过4吨部分 |
3 |
| 超过4吨部分 |
n |
已知某用户1月份用水量为3.5吨，缴纳水费为7.5元；2月份用水量为6吨，缴纳水费为21元.设用户每月缴纳的水费为y元.
(1)写出y关于t的函数关系式；
(2)某用户希望4月份缴纳的水费不超过18元，求该用户最多可以用多少吨水？
为了分析某个高三学生的学习状态，对其下一阶段的学习提供指导性建议．现对他前
次考试的数学成绩
、物理成绩
进行分析．下面是该生次考试的成绩．
| 数学 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
| 物理 |
94 |
91 |
108 |
96 |
104 |
101 |
106 |
（1）他的数学成绩与物理成绩哪个更稳定？请给出你的理由；
（2）已知该生的物理成绩与数学成绩是线性相关的，若该生的物理成绩达到
分，请你估计他的数学成绩大约是多少？
（已知88
94+8391+117108+9296+108104+100101+112106=70497，
）
（参考公式：
，
）
如图，A，B，C，D都在同一个与水平面垂直的平面内，B，D为两岛上的两座灯塔的塔顶．测量船于水面A处测得B点和D点的仰角分别为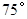
，
，于水面C处测得B点和D点的仰角均为
，
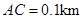．试探究图中B，D间距离与另外哪两点间距离相等，然后求B，D的距离（计算结果精确到
0．01km，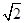
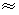1．414，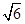
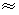2．449）．
设数列{an}满足a1＝2，an＋1－an＝3·4n（n∈N*）．
（1）求数列{an}的通项公式；
（2）令bn＝n+an，求数列{bn}的前n项和Sn．
在△ABC中，角A，B，C的对边分别为a，b，c．已知3cos（B－C）－1＝6cosBcosC．
（1）求cosA；
（2）若a＝3，△ABC的面积为2
，求b，c．
已知函数f（x）＝Asin（ωx＋φ），x∈R，（其中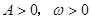
，
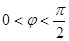）的周期为π，且图象上一个最低点为
．
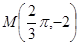（1）求f（x）的解析式；
（2）当x∈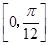
时，求f（x）的最值．