(本题10分)某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30min抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102, 101, 99, 98, 103, 98, 99;
乙:110, 115, 90, 85, 75, 115, 110。
(Ⅰ)这种抽样方法叫做什么抽样方法?
(Ⅱ)将这两组数据用茎叶图表示出来;
(Ⅲ)将两组数据比较:说明哪个车间的产品较稳定。
已知函数 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)设△ 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知 为锐角,
为锐角, ,
, ,
, ,求
,求 的值.
的值.
设函数 ,
, ,
, ,
,
(1)若曲线 与
与 轴相切于异于原点的一点,且函数
轴相切于异于原点的一点,且函数 的极小值为
的极小值为 ,求
,求 的值;
的值;
(2)若 ,且
,且 ,
,
①求证: ; ②求证:
; ②求证: 在
在 上存在极值点.
上存在极值点.
如图,两条相交线段 、
、 的四个端点都在椭圆
的四个端点都在椭圆 上,其中,直线
上,其中,直线 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 .
.
(1)若 ,
, ,求
,求 的值;
的值;
(2)探究:是否存在常数 ,当
,当 变化时,恒有
变化时,恒有 ?
?
如图,四棱锥 的底面ABCD是平行四边形,
的底面ABCD是平行四边形, ,
, ,
, 面
面 ,设
,设 为
为 中点,点
中点,点 在线段
在线段 上且
上且 .
.
(1)求证: 平面
平面 ;
;
(2)设二面角 的大小为
的大小为 ,若
,若 ,求
,求 的长.
的长.
设数列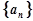 的前n项和为
的前n项和为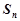 ,
,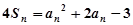 ,且
,且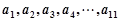 成等比数列,当
成等比数列,当 时,
时,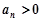 .
.
(1)求证:当 时,
时, 成等差数列;
成等差数列;
(2)求 的前n项和
的前n项和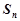 .
.