（本题12分）直线l:y=kx＋1与双曲线C:
的右支交于不同的两点A,B.
（Ⅰ）求实数k的取值范围；
（Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？若存在，求出k的值；若不存在，说明理由.
（本小题满分12分） 惠州市某校中学生篮球队假期集训，集训前共有6个篮球，其中3个是新球（即没有用过的球），3个是旧球（即至少用过一次的球）．每次训练都从中任意取出2个球，用完后放回．
（1）设第一次训练时取到的新球个数为
，求的分布列和数学期望；
（2）已知第一次训练时用过的球放回后都当作旧球，求第二次训练时恰好取到
个新球的概率．
参考公式：互斥事件加法公式：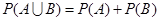
（事件
与事件
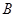互斥）．
独立事件乘法公式：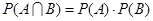
（事件与事件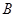相互独立）．
条件概率公式：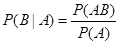
．
（本小题满分12分）已知函数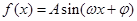
，
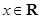（其中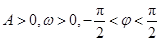
），其部分图像如图所示．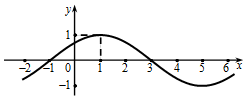
（1）求函数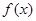
的解析式；
（2）已知横坐标分别为
、
、
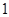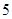的三点
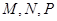都在函数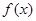的图像上，求
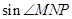的值．
（本小题满分13分）对于函数
，如果它们的图象有公共点P，且在点P处的切线相同，则称函数
和
在点P处相切，称点P为这两个函数的切点.设函数
,
.
（Ⅰ）当
,
时,判断函数和是否相切？并说明理由；
（Ⅱ）已知
，
，且函数和相切，求切点P的坐标；
（Ⅲ）设，点P的坐标为
，问是否存在符合条件的函数和，使得它们在点P处相切？若点P的坐标为
呢？（结论不要求证明）
（本小题满分14分）已知椭圆C：
的右焦点为F，右顶点为A，离心率为e，点
满足条件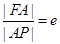
.
（Ⅰ）求m的值；
（Ⅱ）设过点F的直线l与椭圆C相交于M，N两点，记
和
的面积分别为
，
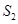，若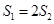
,求直线l的方程.
（本小题满分13分）最近，张师傅和李师傅要将家中闲置资金进行投资理财. 现有两种投资方案，且一年后投资盈亏的情况如下：
（1）投资股市：
| 投资结果 |
获利 |
不赔不赚 |
亏损 |
| 概率 |
 |
 |
 |
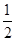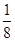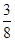（2）购买基金：
| 投资结果 |
获利 |
不赔不赚 |
亏损 |
| 概率 |
 |
 |
 |
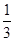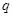（Ⅰ）当
时，求q的值；
（Ⅱ）已知“购买基金”亏损的概率比“投资股市”亏损的概率小，求
的取值范围；
（Ⅲ）已知张师傅和李师傅两人都选择了“购买基金”来进行投资，假设三种投资结果出现的可能性相同，求一年后他们两人中至少有一人获利的概率．