(本小题满分12分)
设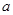 ∈R,函数
∈R,函数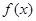 =
=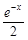 (
(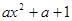 ),其中e是自然对数的底数.
),其中e是自然对数的底数.
(1)判断f (x)在R上的单调性;
(2)当– 1 <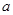 < 0时,求f (x)在[1,2]上的最小值.
< 0时,求f (x)在[1,2]上的最小值.
选做题:请考生从给出的3道题中任选一题做答,并在答题卡上把所选题目的题号用2B铅笔涂黑.注意所做题目的题号必须与所涂的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.
已知椭圆的一个顶点为A(0,-1),焦点在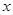 轴上,若右焦点到直线
轴上,若右焦点到直线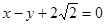 的距离为3.
的距离为3.
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆与直线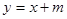 相交于不同的两点M、N,问是否存在实数
相交于不同的两点M、N,问是否存在实数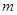 使
使 ;若存在求出
;若存在求出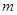 的值;若不存在说明理由。
的值;若不存在说明理由。
在平面直角坐标系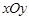 中,直线
中,直线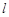 与抛物线
与抛物线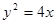 相交于不同的两点
相交于不同的两点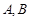 .
.
(Ⅰ)如果直线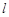 过抛物线的焦点,求
过抛物线的焦点,求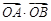 的值;
的值;
(Ⅱ)在此抛物线上求一点P,使得P到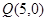 的距离最小,并求最小值.
的距离最小,并求最小值.
已知半径为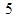 的圆的圆心M在
的圆的圆心M在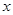 轴上,圆心M的横坐标是整数,且圆M与直线
轴上,圆心M的横坐标是整数,且圆M与直线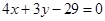 相切.
相切.
求:(Ⅰ)求圆M的方程;
(Ⅱ)设直线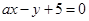 与圆M相交于
与圆M相交于 两点,求实数
两点,求实数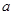 的取值范围.
的取值范围.
(本小题满分14分)已知:定义在R上的函数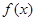 ,对于任意实数a, b都满足
,对于任意实数a, b都满足 ,且
,且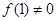 ,当
,当 .
.
(Ⅰ)求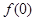 的值;
的值;
(Ⅱ)证明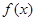 在
在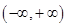 上是增函数;
上是增函数;
(Ⅲ)求不等式 的解集.
的解集.
(本小题满分14分)已知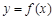 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时,
时, .
.
(Ⅰ)求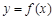 的解析式;
的解析式;
(Ⅱ)问是否存在这样的正数a, b使得当 时,函数
时,函数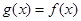 的值域为
的值域为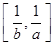 ,若存在,求出所有a, b的值,若不存在,说明理由.
,若存在,求出所有a, b的值,若不存在,说明理由.