(本小题满分12分)
正四棱柱ABCD-A1B1C1D1的底面边长是 ,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
(1)求证:A1C⊥面AEF;
(2)求截面AEF与底面ABCD所成二面角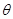 的正切值.
的正切值.
已知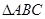 的三内角
的三内角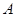 、
、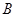 、
、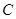 所对的边分别是
所对的边分别是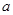 ,
,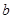 ,
,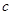 ,且
,且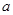 ,
,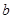 ,
,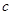 成等比数列。
成等比数列。
(1)若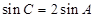 ,求
,求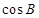 的值;
的值;
(2)求角B的最大值,并判断此时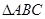 的形状
的形状
已知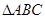 的三内角
的三内角 、
、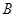 、
、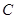 所对的边分别是
所对的边分别是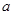 ,
, ,
, ,向量
,向量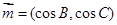
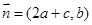 ,且
,且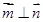 。
。
(1)求角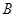 的大小;
的大小;
(2)若 ,求
,求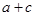 的范围。
的范围。
已知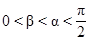 ,
,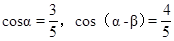
(1)求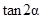 ;
;
(2)求 。
。
已知函数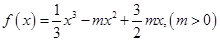 。
。
(1)当 时,①求函数
时,①求函数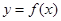 的单调区间;②求函数
的单调区间;②求函数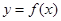 的图象在点
的图象在点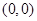 处的切线方程;
处的切线方程;
(2)若函数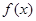 既有极大值,又有极小值,且当
既有极大值,又有极小值,且当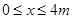 时,
时,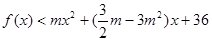 恒成立,求
恒成立,求 的取值范围.
的取值范围.
如图,椭圆
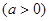 的焦点在x轴上,左右顶点分别为
的焦点在x轴上,左右顶点分别为 ,上顶点为B,抛物线
,上顶点为B,抛物线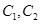 分别以A,B为焦点,其顶点均为坐标原点O,
分别以A,B为焦点,其顶点均为坐标原点O, 与
与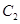 相交于直线
相交于直线 上一点P.
上一点P.
(1)求椭圆C及抛物线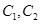 的方程;
的方程;
(2)若动直线 与直线OP垂直,且与椭圆C交于不同的两点M,N,已知点
与直线OP垂直,且与椭圆C交于不同的两点M,N,已知点 ,求
,求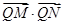 的最小值.
的最小值.