平面直角坐标系中,已知椭圆:的离心率为,且点(,)在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆:,为椭圆上任意一点,过点的直线交椭圆于两点,射线交椭圆于点.
(ⅰ)求的值;
(ⅱ)求面积的最大值.
已知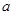 为实数,函数
为实数,函数 .
.
(1)若 ,求
,求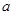 的值及曲线
的值及曲线 在
在 处的切线方程;
处的切线方程;
(2)求 在区间
在区间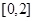 上的最大值.
上的最大值.
如图,在四棱锥 中,
中, ,
,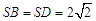 ,底面
,底面 是菱形,且
是菱形,且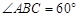 ,
,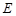 为
为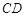 的中点.
的中点.
(1)求四棱锥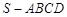 的体积;
的体积;
(2)侧棱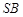 上是否存在点
上是否存在点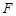 ,使得
,使得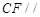 平面
平面 ?并证明你的结论.
?并证明你的结论.
已知 ,
,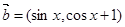 ,函数
,函数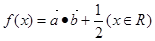
(1)求函数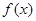 的周期;
的周期;
(2)函数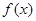 的图像可由函数
的图像可由函数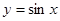 的图像经过怎样的变换得到?
的图像经过怎样的变换得到?
如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000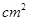 ,四周空白的宽度为10
,四周空白的宽度为10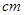 ,两栏之间的中缝空白的宽度为5
,两栏之间的中缝空白的宽度为5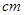 ,怎样确定广告的高与宽的尺寸(单位:
,怎样确定广告的高与宽的尺寸(单位: ),能使矩形广告面积最小?
),能使矩形广告面积最小?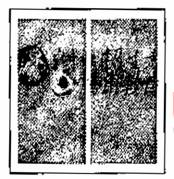
如图所示的长方体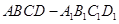 中,底面
中,底面 是边长为
是边长为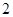 的正方形,
的正方形,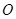 为
为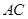 与
与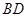 的交点,
的交点,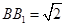 ,
, 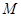 是线段
是线段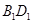 的中点.
的中点.
(1)求证: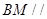 平面
平面 ;
;
(2)求三棱锥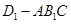 的体积.
的体积.