(本小题满分12分)
已知数列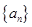 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数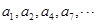 构成等差数列
构成等差数列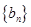 ,
,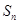 是
是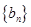 的前n项和,且
的前n项和,且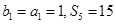
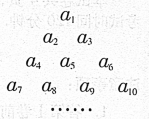
( I )若数阵中从第三行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知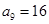 ,求
,求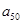 的值;
的值;
(Ⅱ)设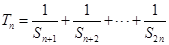 ,求
,求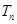 .
.
已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为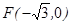 ,且过
,且过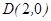 ,设点
,设点 .
.
(1)求该椭圆的标准方程;
(2)若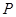 是椭圆上的动点,求线段
是椭圆上的动点,求线段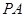 中点
中点 的轨迹方程。
的轨迹方程。
(本小题满分8分) 某车间生产某机器的两种配件A和B,生产配件A成本费y 与该车间的工人人数x成反比,而生产配件B成本费y
与该车间的工人人数x成反比,而生产配件B成本费y 与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y
与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y 和y
和y 分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
如图,P—ABCD是正四棱锥,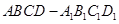 是正方体,其中
是正方体,其中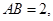


(1)求证: ;
;
(2)求平面PAD与平面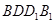 所成的锐二面角
所成的锐二面角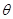 的余弦值;
的余弦值;
(本小题满分10分)已知:等差数列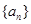 ,
, ,前
,前 项和为
项和为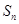 .各项均为正数的等比数列列
.各项均为正数的等比数列列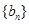 满足:
满足: ,
, ,且
,且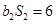 .
.
(1)求数列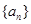 与
与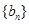 的通项公式;
的通项公式;
(Ⅱ)求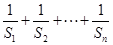
(本小题满分10分) 在 中,角
中,角 的对边分别为
的对边分别为 ,且满足
,且满足

(1)求角 的大小;
的大小;
(2)若 为钝角三角形,求实数
为钝角三角形,求实数 的取值范围。
的取值范围。