(本小题满分10分)
命题p:对任意实数 都有
都有 恒成立;命题q :关于
恒成立;命题q :关于 的方程
的方程 有实数根.若“p或q”为真命题,“p且q”为假命题,求实数
有实数根.若“p或q”为真命题,“p且q”为假命题,求实数 的取值范围。
的取值范围。
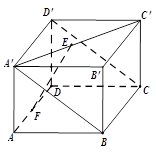
(本小题满分12分)如图所示,在长方体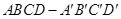 中,
中,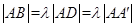 ,(
,(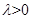 ),
),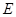 、
、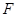 分别是
分别是 和
和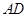 的中点,且
的中点,且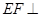 平面
平面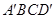 .
.
(1)求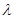 的值;
的值;
(2)求二面角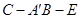 的余弦值.
的余弦值.
(本小题满分12分)已知各项不为零的数列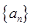 的前
的前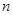 项和为
项和为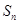 ,且满足
,且满足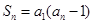 .
.
(1)求数列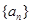 的通项公式;
的通项公式;
(2)设数列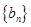 满足
满足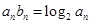 ,求数列
,求数列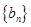 的前
的前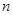 项和
项和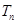 .
.
(本小题满分12分)某电视台有一档综艺节目,其中有一个抢答环节,有甲、乙两位选手进行抢答,规则如下:若选手抢到答题权,答对得20分,答错或不答则送给对手10分。已知甲、乙两位选手抢到答题权的概率均相同,且每道题是否答对的机会是均等的, 若比赛进行两轮.
(1)求甲抢到1题的概率;
(2)求甲得到10分的概率.
(本小题满分12分)已知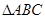 的三个内角A、B、C的对边分别为
的三个内角A、B、C的对边分别为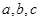 ,且
,且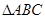 的面积
的面积 .
.
(1)求角B的大小;
(2)若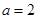 ,且
,且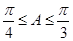 ,求边
,求边 的取值范围.
的取值范围.
(本小题满分10分)选修4-5:不等式选讲
(1)已知 ,求
,求 的取值范围;
的取值范围;
(2)若对任意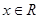 ,
, 恒成立,求
恒成立,求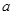 的取值范围.
的取值范围.