(本小题满分12分)
命题 实数x满足
实数x满足 (其中
(其中 ),命题
),命题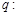 实数
实数 满足
满足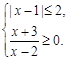
(1)若 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若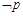 是
是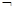
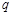 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
设双曲线 的两个焦点分别为
的两个焦点分别为 、
、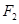 ,离心率为2.
,离心率为2.
(1)求双曲线的渐近线方程;
(2)过点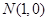 能否作出直线
能否作出直线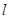 ,使
,使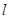 与双曲线
与双曲线 交于
交于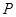 、
、 两点,且
两点,且 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.
某种型号的汽车在匀速行驶中每小时耗油量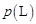 关于行驶速度
关于行驶速度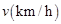 的函数解析式可以表示为:
的函数解析式可以表示为: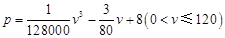 .已知甲、乙两地相距
.已知甲、乙两地相距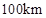 ,设汽车的行驶速度为
,设汽车的行驶速度为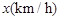 ,从甲地到乙地所需时间为
,从甲地到乙地所需时间为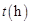 ,耗油量为
,耗油量为 .
.
(1)求函数 及
及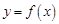 ;
;
(2)求当 为多少时,
为多少时, 取得最小值,并求出这个最小值.
取得最小值,并求出这个最小值.
已知函数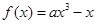 ,其中
,其中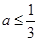 .
.
(1)当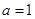 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)求函数 在
在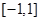 上的最大值.
上的最大值.
椭圆 的左、右焦点分别为
的左、右焦点分别为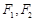 ,一条直线
,一条直线 经过点
经过点 与椭圆交于
与椭圆交于 两点.
两点.
⑴求 的周长;
的周长;
⑵若 的倾斜角为
的倾斜角为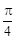 ,求
,求 的面积.
的面积.
已知 ,设命题
,设命题 :不等式
:不等式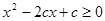 解集为R;命题
解集为R;命题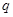 :方程
:方程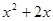
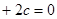 没有实根,如果命题p或q为真命题,p且q为假命题,求
没有实根,如果命题p或q为真命题,p且q为假命题,求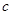 的取值范围.
的取值范围.