(本小题满分12分,(Ⅰ)小问3分,(Ⅱ)小问9分.)
直线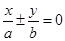 称为椭圆
称为椭圆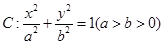 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率 .(1)求椭圆的“特征直线”方程;
.(1)求椭圆的“特征直线”方程;
(2)过椭圆C上一点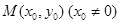 作圆
作圆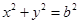 的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若
的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若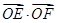 取值范围恰为
取值范围恰为 ,求椭圆C的方程.
,求椭圆C的方程.
(本小题满分12分)已知命题p:∀x∈[1,2],x2-a 0.命题q:∃x0∈R,使得x02+(a-1)x0+1=0.若“p或q”为真,“p且q”为假,求实数a的取值范围.
0.命题q:∃x0∈R,使得x02+(a-1)x0+1=0.若“p或q”为真,“p且q”为假,求实数a的取值范围.
(本小题满分12分)设数列 的前
的前 项和为
项和为 ,数列
,数列 为等比数列,且
为等比数列,且 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
如图,在三棱锥 中,
中,  平面
平面 ,
,  ,
,  ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)求证: ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)求点 到平面
到平面 的距离.
的距离.
如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).
(1)求证:平面EFG∥平面PAB;
(2)若点Q是线段PB的中点,求证:PC⊥平面ADQ;
(3)求三棱锥C-EFG的体积.
如图, 是半径为
是半径为 的半圆,
的半圆,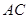 为直径,点
为直径,点 为
为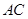 的中点,点
的中点,点 和点
和点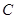 为线段
为线段 的三等分点,平面
的三等分点,平面 外一点
外一点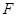 满足
满足 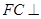 平面
平面 ,
, .
.
(1)证明: ;
;
(2)求点 到平面
到平面 的距离.
的距离.