(本小题满分12分)已知函数 .
.
(1) 若 在
在 处取得极值, 求
处取得极值, 求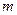 的值;
的值;
(2) 若以函数 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立, 求正实数
恒成立, 求正实数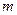 的最小值;
的最小值;
(3) 在(1)的条件下, 若关于 的方程
的方程 在
在 上恰有两个不同的实根, 求实数
上恰有两个不同的实根, 求实数 的取值范围.
的取值范围.
(本小题满分12分)如图,在四棱锥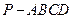 中,
中,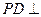 底面
底面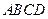 ,底面
,底面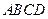 为正方形,
为正方形,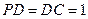 ,
,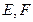 分别是
分别是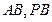 的中点.
的中点.
(1) 求证: 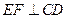 ;
;
(2) 求二面角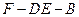 的大小;
的大小;
(3) 在平面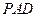 内求一点
内求一点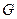 , 使
, 使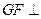 平面
平面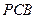 , 并证明你的结论.
, 并证明你的结论.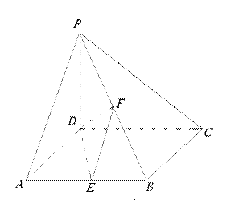
(本小题满分12分)有3个不相同的球和4 个盒子,盒子的编号分别为1、2、3、4,将球逐个独立地、随机地放入4个盒子中去. 以
个盒子,盒子的编号分别为1、2、3、4,将球逐个独立地、随机地放入4个盒子中去. 以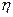 表示其中至少有球的盒子的最小号码.(例如,事件
表示其中至少有球的盒子的最小号码.(例如,事件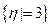 表示第1号,第2号盒子都是空的, 第3号盒子中至少有一个球).
表示第1号,第2号盒子都是空的, 第3号盒子中至少有一个球).
(1) 当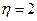 时, 求
时, 求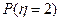 ;(2) 求
;(2) 求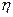 的分布列及期望
的分布列及期望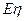 .
.
(本小题满分10分)(注意:在试题卷上作答无效)
已知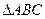 的内角
的内角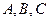 分别对应
分别对应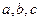 ,向量
,向量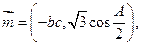
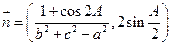 ,且
,且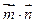 =1.
=1.
(1)求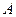 ;
;
(2) 若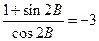 , 求
, 求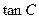
(本小题满分12分)已知焦点为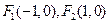 的椭圆经过点
的椭圆经过点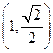 , 直线
, 直线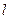 过点
过点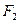 与椭圆交于
与椭圆交于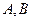 两点, 其中
两点, 其中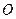 为坐标原点.
为坐标原点.
(1) 求椭圆的方程; (2) 求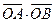 的范围;
的范围;
(3) 若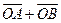 与向量
与向量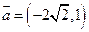 共线, 求
共线, 求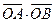 的值及
的值及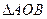 的外接圆方程.
的外接圆方程.