（本题10分） 为了解高二学年女生身高情况，对高二(10)班女生身高进行了一次测量，所得数据整理后列出了频率分布表如下：
| 组 别 |
频数 |
频率 |
| 145.5～149.5 |
1 |
0.02 |
| 149.5～153.5 |
4 |
0.08 |
| 153.5～157.5 |
20 |
0.40 |
| 157.5～161.5 |
15 |
0.30 |
| 161.5～165.5 |
8 |
0.16 |
| 165.5～169.5 |
m |
n |
| 合 计 |
M |
N |
（1）求出表中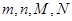
所表示的数分别是多少？
（2）若该校高二学年共有女生500人，试估计高二女生中身高在161.5以上的人数。