(本小题满分12分)
已知椭圆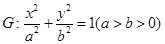 的离心率为
的离心率为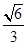 ,右焦点为(
,右焦点为(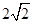 ,0),斜率为1的直线
,0),斜率为1的直线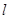 与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为
与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为 .
.
(1)求椭圆G的方程;
(2)求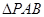 的面积.
的面积.
在如图的几何体中,平面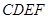 为正方形,平面
为正方形,平面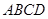 为等腰梯形,
为等腰梯形,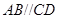 ,
,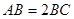 ,
,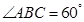 ,
,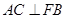 .
.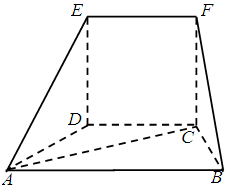
(1)求证: 平面
平面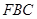 ;
;
(2)求直线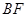 与平面
与平面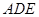 所成角的正弦值.
所成角的正弦值.
空气质量指数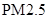 (单位:
(单位: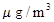 )表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.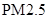 的浓度与空气质量类别的关系如下表所示:
的浓度与空气质量类别的关系如下表所示:
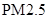 日均浓度 日均浓度 |
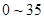 |
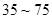 |
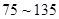 |
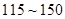 |
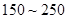 |
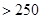 |
| 空气质量类别 |
优 |
良 |
轻度污染 |
中度污染 |
重度污染 |
严重污染 |
从甲城市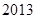 年
年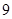 月份的
月份的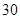 天中随机抽取
天中随机抽取 天的
天的 日均浓度指数数据茎叶图如图5所示.
日均浓度指数数据茎叶图如图5所示.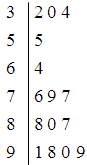
(1)试估计甲城市在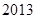 年
年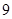 月份的
月份的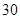 天的空气质量类别为优或良的天数;
天的空气质量类别为优或良的天数;
(2)在甲城市这 个监测数据中任取
个监测数据中任取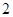 个,设
个,设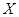 为空气质量类别为优或良的天数,求
为空气质量类别为优或良的天数,求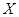 的分布列及数学期望.
的分布列及数学期望.
)在△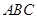 中,角
中,角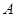 、
、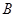 、
、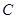 所对的边分别为
所对的边分别为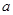 、
、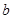 、
、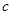 ,且
,且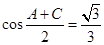 .
.
(1)求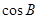 的值;
的值;
(2)若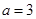 ,
,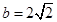 ,求
,求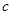 的值.
的值.
已知函数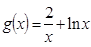 ,
,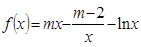 ,
,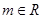 .
.
(1)求函数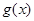 的极值点;
的极值点;
(2)若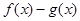 在
在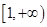 上为单调函数,求
上为单调函数,求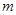 的取值范围;
的取值范围;
(3)设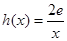 ,若在
,若在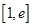 上至少存在一个
上至少存在一个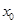 ,使得
,使得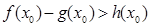 成立,求
成立,求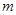 的取值范围.
的取值范围.
已知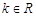 ,函数
,函数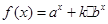
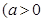 且
且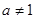 ,
,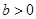 且
且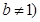 .
.
(1) 如果实数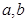 满足
满足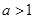 且
且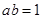 ,函数
,函数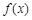 是否具有奇偶性? 如果有,求出相应的
是否具有奇偶性? 如果有,求出相应的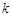 值;如果没有,说明原因;
值;如果没有,说明原因;
(2) 如果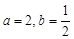 ,讨论函数
,讨论函数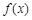 的单调性。
的单调性。