(本小题共12分)
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
| 月收入(单位百元) |
[15,25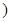 |
[25,35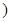 |
[35,45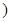 |
[45,55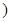 |
[55,65 |
[65,75 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(1)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
| |
月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
| 赞成 |
 |
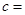 |
|
| 不赞成 |
 |
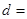 |
|
| 合计 |
|
|
|
(2)若对在[15,25) ,[25,35)的被调查中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为 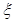 ,求随机变量
,求随机变量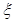 的分布列。
的分布列。
附:

有一枚正方体骰子,六个面分别写1、2、3、4、5、6的数字,规定“抛掷该枚骰子得到的数字是抛掷后,面向上的那一个数字”.已知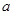 和
和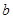 是先后抛掷该枚骰子得到的数字,函数
是先后抛掷该枚骰子得到的数字,函数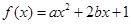
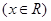
(1)若先抛掷骰子得到的数字是3,求再次抛掷骰子时,使函数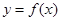 有零点的概率;
有零点的概率;
(2)求函数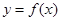 在区间(-3,+∞)上是增函数的概率.
在区间(-3,+∞)上是增函数的概率.
已知定义在 上的函数
上的函数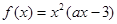 ,其中
,其中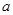 为常数.
为常数.
(1)若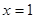 是函数
是函数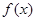 的一个极值点,求
的一个极值点,求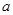 的值;
的值;
(2)若函数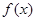 在区间
在区间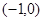 上是增函数,求
上是增函数,求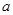 的取值范围.
的取值范围.
已知数列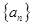 :
: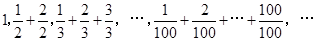
(1)观察规律,写出数列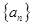 的通项公式,它是个什么数列?
的通项公式,它是个什么数列?
(2)若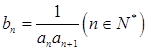 ,设
,设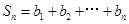 ,求
,求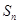 。
。
(3)设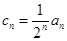 ,
, 为数列
为数列 的前
的前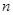 项和,求
项和,求 。
。
在△ABC中,角 所对的边分别是
所对的边分别是 ,且
,且 。
。
(1)求 的值;
的值;
(2)若 ,
, 的面积
的面积 ,求
,求 的值。
的值。
已知 的解集为
的解集为 ,求不等式
,求不等式 的解集.
的解集.