某零售店近五个月的销售额和利润额资料如下表:
| 商店名称 |
A |
B |
C |
D |
E |
销售额 (千万元) (千万元) |
3 |
5 |
6 |
7 |
9 9 |
利润额 (百万元) (百万元) |
2 |
3 |
3 |
4 |
5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额 关于销售额
关于销售额 的回归直线方程;
的回归直线方程;
(3)当销售额为4(千万元)时,利用(2)的结论估计该零售店的利润额(百万元).
设某市现有从事第二产业人员100万人,平均每人每年创造产值a万元(a为正常数),现在决定从中分流x万人去加强第三产业。分流后,继续从事第二产业的人员平均每人每年创造产值可增加2x%(0<x<100)。而分流出的从事第三产业的人员,平均每人每年可创造产值1.2a万元。
(1)若要保证第二产业的产值不减少,求x的取值范围;
(2)在(1)的条件下,问应分流出多少人,才能使该市第二、三产业的总产值增加最多?
(1)已知 ,求函数
,求函数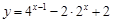 的最大值和最小值;
的最大值和最小值;
(2)要使函数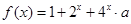 在
在 上f (x)
上f (x) 恒成立,求a的取值范围.
恒成立,求a的取值范围.
已知命题p:对m∈[-1,1],不等式a2-5a+3≥ 恒成立;命题q:方程x2+ax+4=0在实数集内没有解;若p和q都是真命题,求a的取值范围.
恒成立;命题q:方程x2+ax+4=0在实数集内没有解;若p和q都是真命题,求a的取值范围.
若集合 ,
, 且
且
(1)若 ,求集合
,求集合 ;
;
(2)若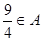 ,求
,求 的取值范围.
的取值范围.
记函数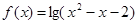 的定义域为集合A,函数
的定义域为集合A,函数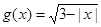 的定义域为集合B.
的定义域为集合B.
(1)求A∩B和A∪B;
(2)若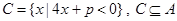 ,求实数
,求实数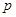 的取值范围.
的取值范围.