(本小题满分12分)
已知a为实数,
(1)求导数 ;
;
(2)若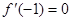 ,求
,求 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;
(本小题8分) 设函数 (常数
(常数
(1)求 的定义域;
的定义域;
(2)在函数 的图像上是否存在不同的两点,使得过这两点的直线平行于x轴?
的图像上是否存在不同的两点,使得过这两点的直线平行于x轴?
(3)当 满足什么条件时,
满足什么条件时, 在
在 上恒取正值。
上恒取正值。
(本小题8分) 嘉兴市秀洲区为促进淡水鱼养殖业的发展,将价格控制在适当范围内,并决定对淡水鱼养殖提供政府补贴。设淡水鱼的市场价格为 ,政府补贴为
,政府补贴为 。根据市场调查,当
。根据市场调查,当 时,淡水鱼的
时,淡水鱼的 市场日供应
市场日供应 量
量 与市场日需求量
与市场日需求量 近似满足关系:
近似满足关系: ,
, ;当
;当 时的市场价格称为市场平衡价格。
时的市场价格称为市场平衡价格。
(1)将政府补贴费表示为市场平衡价格的函数,并求出函数的定义域;
(2)为使市场平衡价格不高于 ,政府需要补贴吗?如果需要,至少为多少
,政府需要补贴吗?如果需要,至少为多少 ?
?
若 是定义在
是定义在 上的增函数,且对一切
上的增函数,且对一切 满足
满足
(1)求
(2)若 ,解不等式
,解不等式
(本小题7分)已知集合 ,若(
,若(
 .求实数
.求实数 的取值范围.
的取值范围.
设函数 ,其中
,其中 .⑴若
.⑴若 的定义域为区间
的定义域为区间 ,求
,求 的最
的最
大值和最小值;⑵若 的定义域为区间
的定义域为区间 ,求
,求 的取值范围,使
的取值范围,使 在定义域
在定义域
内是单调减函数。