如图，在平行六面体ABCD-A1B1C1D1中，四边形ABCD与四边形CC1D1D均是边长为1的正方形，∠ADD1="120°" ，点E为A1B1的中点，点P，Q分别是BD，CD1上的动点，且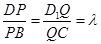
.
（1）当平面PQE//平面ADD1A1时，求
的值.
（2）在（1）的条件下，求直线QE与平面DQP所成角的正弦值.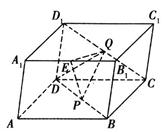
已知等差数列{an}的前n项和为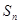
(I)若a1=1，S10= 100，求{an}的通项公式;
(II)若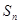=n2-6n，解关于n的不等式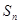+ an >2n
已知函数
，
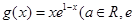为自然对数的底数）.
(Ⅰ)当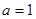
时,求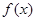
的单调区间；
(Ⅱ)若函数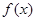在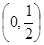
上无零点,求
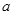最小值；
(Ⅲ)若对任意给定的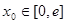
,在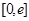
上总存在两个不同的
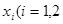),使
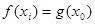成立,求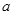的取值范围.
给定椭圆C：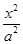
＋
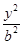＝1(a>b>0)，称圆心在原点O，半径为
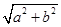的圆是椭圆C的“准圆”．若椭圆C的一个焦点为F(
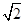，0)，且其短轴上的一个端点到F的距离为
.
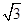(Ⅰ)求椭圆C的方程和其“准圆”方程；
(Ⅱ)点P是椭圆C的“准圆”上的一个动点，过动点P作直线l1，l2，使得l1，l2与椭圆C都只有一个交点，试判断l1，l2是否垂直，并说明理由．
已知函数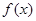
＝x2＋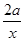
(a∈R)．
(Ⅰ)若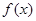在x＝1处的切线垂直于直线x－14y＋13＝0，求该点的切线方程，并求此时函数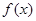的单调区间；
(Ⅱ)若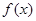≤a2－2a＋4对任意的x∈[1,2]恒成立，求实数a的取值范围．
如图，四棱锥P－ABCD中，PA⊥底面ABCD，四边形ABCD中，AB⊥AD，AB＋AD＝4，CD＝
，∠CDA＝45°.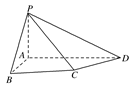
(Ⅰ)求证：平面PAB⊥平面PAD；
(Ⅱ)设AB＝AP．
(ⅰ) 若直线PB与平面PCD所成的角为30°，求线段AB的长；
(ⅱ) 在线段AD上是否存在一个点G，使得点G到点P，B，C，D的距离都相等？说明理由．