在直角坐标系中,设函数 , 是常数, .
(1)若该函数的图象经过 和 两点,求函数的表达式,并写出函数图象的顶点坐标;
(2)写出一组 , 的值,使函数 的图象与 轴有两个不同的交点,并说明理由.
(3)已知 ,当 , , 是实数, 时,该函数对应的函数值分别为 , .若 ,求证: .
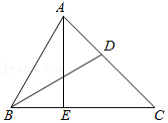
如图,在 中, 的平分线 交 边于点 , 于点 .已知 , .
(1)求证: ;
(2)若 ,求 的面积.
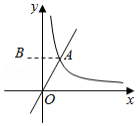
在直角坐标系中,设函数 是常数, , 与函数 是常数, 的图象交于点 ,点 关于 轴的对称点为点 .
(1)若点 的坐标为 ,
①求 , 的值;
②当 时,写出 的取值范围;
(2)若点 在函数 是常数, 的图象上,求 的值.
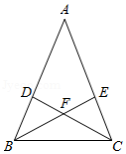
在① ,② ,③ 这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.
问题:如图,在 中, ,点 在 边上(不与点 ,点 重合),点 在 边上(不与点 ,点 重合),连接 , , 与 相交于点 .若 ① ② 或 ③ ,求证: .
注:如果选择多个条件分别作答,按第一个解答计分.
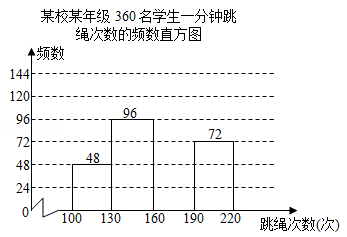
为了解某校某年级学生一分钟跳绳情况,对该年级全部360名学生进行一分钟跳绳次数的测试,并把测得数据分成四组,绘制成如图所示的频数表和未完成的频数分布直方图(每一组不含前一个边界值,含后一个边界值).
某校某年级360名学生一分钟跳绳次数的频数表
|
组别(次 |
频数 |
|
|
48 |
|
|
96 |
|
|
|
|
|
72 |
(1)求 的值;
(2)把频数分布直方图补充完整;
(3)求该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比.