(本小题满分12分)
已知函数 .
.
(Ⅰ)讨论函数 在
在 上的单调性;
上的单调性;
(Ⅱ)设 ,且
,且 ,求
,求 的值.
的值.
已知圆x2+y2=1和双曲线(x-1)2-y2=1,直线l与双曲线交于不同两点A、B,且线段AB的中点恰是l与圆相切的切点,求直线l的方程.
已知椭圆C的方程为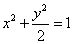 ,点P(a,b)的坐标满足
,点P(a,b)的坐标满足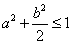 ,过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:
,过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:
(1)点Q的轨迹方程.
(2)点Q的轨迹与坐标轴的交点的个数.
对于数列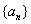 ,规定数列
,规定数列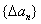 为数列
为数列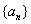 的一阶差分数列,其中
的一阶差分数列,其中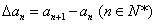 ;一般地,规定
;一般地,规定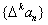 为
为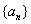 的k阶差分数列,其中
的k阶差分数列,其中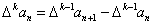 且k∈N*,k≥2。
且k∈N*,k≥2。
(1)已知数列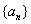 的通项公式
的通项公式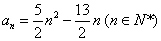 。试证明
。试证明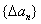 是等差数列;
是等差数列;
(2)若数列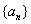 的首项a1=―13,且满足
的首项a1=―13,且满足 ,求数列
,求数列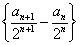 及
及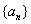 的通项公式;
的通项公式;
(3)在(2)的条件下,判断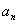 是否存在最小值;若存在,求出其最小值,若不存在,说明理由。
是否存在最小值;若存在,求出其最小值,若不存在,说明理由。
已知{an}是公比为q的等比数列,且a1,a3,a2成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.